 (a) Actual dependences
(a) Actual dependences
|
 (b) dependence graph
(b) dependence graph
|
 (c) Dependence stack
(c) Dependence stack
|
Like memory management, DSI provides complete process management. We begin this chapter with a description of the key events in a suspension's life-cycle: process creation, activation and termination. This provides a basis for a discussion of higher level process management issues: synchronization, scheduling, controlling parallelism, and speculative computation.
All suspensions are created with the suspend instruction, which initializes suspension records in the heap. The created suspension inherits some of its fields from the registers of the context window of the currently running process; the new suspension record can be swapped directly in and out of a context window to instantiate the process. Most suspensions require a convergence context to be useful: a cell in the heap containing the suspension reference that is the location for storing the manifest result of computing the suspended computation. A process executing a typical suspending construction code sequence will execute one or more suspend instructions interspersed with new instructions in building a data structure.
A suspension is activated in one of two ways:
A scheduled suspension is considered an active process. The kernel resumes an active suspension by loading it into an open context window and transferring control to that window. The suspension resumes execution at the control point in the K register. A suspension in this state is a running process. Note that there may be any number of active processes on a given node, some of which are swapped into context windows. There is only one running process per node, namely, the one in a context window that has control of the processor.
The end result of a suspension's execution is almost invariably to compute a value which replaces its own reference in the heap, an operation known as converging to a value. If the suspension is not referenced from another location this causes the suspension to un-reference itself; its state will be recovered at the next garbage collection. Converging is normally accomplished by a sting (store) operation followed by a converge system call, which signals a process' intention to terminate. The kernel responds by swapping the suspension out of its context window and selecting another active suspension to run.
Sometimes, a suspension may store a value that extends the structure of the convergence context, and embeds itself farther down in the structure. For example, the code for an iterating stream process might append items to the tail of a list and then resuspend itself at the new end of the stream. This resuspend behavior is accomplished with the detach operation, a system call which is similar to converge, but has the effect of resetting the control register K such that if and when the suspension is reactivated it resumes execution at the specified control point. Thus, detach is essentially a call to relinquish the processor.
How we implement this dependence synchronization can have a dramatic effect on performance. Our choices fall into two broad categories: polling and blocking synchronization. The difference between these two methods is primarily in where the responsibility lies for rescheduling A. In a polling implementation, the system either periodically wakes up Ato reattempt its probe, or checks B's convergence cell on behalf of Aat some interval, rescheduling Awhen a manifest value has appeared. With blocking synchronization, Ais blocked indefinitely (removed from the schedule) and the act of rescheduling Ais associated with B's convergence.
Both synchronization methods have their strengths and weaknesses:
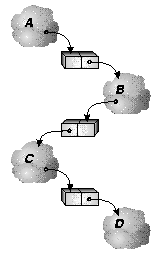
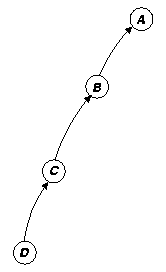
Because of the lazy nature of suspending construction, dependence chains can grow hundreds or thousands of processes deep. Assuming that we are going to do explicit synchronization, we need to track these dependences with an actual structure that mirrors, but reverses, the dynamically unfolding chain of dependences. We depict our reverse dependence graph like a normal dependence graph, only with the arrows reversed, as in figure 14c. Using our dynamically constructed reverse dependence graph we can easily determine which processes should be resumed when a given process converges. The main problem with this approach is maintaining an accurate mapping between our reverse dependence graph (an actual structure that the system manipulates) with the dynamically changing state of actual dependences in the system. As we shall see, this assumption can be problematic, especially in the presence of speculative computation (section 6.7).
Our dependence stack then, is a layer of scheduling infrastructure laid out over the computation as it unfolds. Probes result in pushes, and convergence results in pops; we assume that the process at the top of the stack is the next ready process in that dependence stack.
Dependence stacks are the basic scheduling handles used by the system. When a probe results in a suspension the kernel pushes the dependence stack (as described above) and then examines the suspension reference. If the suspension is local it can proceed to swap it in and execute it. If it is a remote suspension, the kernel sends a scheduling message to the remote processor containing a pointer to the dependence stack, and moves on to examine messages in its own scheduling queues (see section 4.3). When the remote processor gets around to processing this message, it loads the suspension reference from the top of the stack and proceeds to swap it in and execute it. If that suspension probes yet another suspension the same scenario recurs. When a process converges, the kernel pops the dependence stack and checks the suspension reference at the top. If it is a local reference, the suspension is swapped in and executed. If it is nonlocal, the dependence stack is sent to the remote processor and the current processor looks for other stacks in its message queues.
What we have just described is the basic mechanism for distributed demand-driven scheduling in DSI. The fringe of the computation corresponding to a particular dependence chain shifts from processor to processor to take advantage of locality of execution for whichever suspension is currently pushing the fringe. The cost of this scheduling communication is discussed in chapter 4; it is considerably less than the cost of context swapping over the network, which would involve the loading and storing of suspension contexts, perhaps multiple times, plus any additional overhead due to non-local stack manipulation, etc. For details refer to section 5.2.3.
It might seem logical to create and assign a dependence stack to each processor; if each processor is busy handling a stack the entire machine is utilized. Actually, we want multiple pending stacks for each processor. The reason is due to our requirement that suspensions execute locally; if a processor passes its current dependence stack to another node we do not want it to be idle. Rather, it should take up any dependence stacks that have been passed to it from other processors. Given a balanced distribution of suspensions and a small backlog of waiting dependence stacks, any processor should always have work to do. Kranz [DAKM89] briefly discusses the merits this kind of task backlog.
Dynamic parallelism is created in response to explicit
scheduling requests by concurrent primitives.
These requests are the source of branching in the dependence
graph.
Each branch forms a new dependence chain;
the amount and type of branching is determined by the primitive,
and possibly by the number of suspensions in its argument.
For example, consider a hypothetical primitive, pcoerce,
that implements a form of parallel coercion,
scheduling each suspension in its argument list and returning when
they have all converged.
Concurrent primitives are the primary source of parallelism in Daisy. This is consistent with the underlying philosophy of the language; namely, that list construction produces suspended processes, and primitives coerce those processes is various ways (including in parallel). See section 2.3 for details.
One technique to constraining parallelism is to tie process creation (i.e. granularity) to the load of the machine [GM84,Moh90]. For explicitly eager parallel languages (e.g. futures), this may be possible. For Daisy, the laziness of suspensions is a semantic requirement; there is no way to randomly ``inline'' a suspension without changing the semantics of the language6.1. Note that for lazy tasks, it is not the actual creation of tasks that leads to excess parallelism but rather the excess scheduling of tasks (i.e. by primitives). However, that there are other valid reasons to reduce granularity. This is discussed further in section 6.9.
With this in mind, we might consider tying process scheduling to current load conditions. For example, if the load is heavy, pcoerce might only schedule some of its suspensions in parallel, and coerce the others serially. However, since suspensions can only run locally, this would require pcoerce to access the load conditions of all the processors on which it might need to schedule suspensions. This would mean an unacceptable amount of overhead, in addition to placing the burden of these decisions on the surface language. Instead, DSI follows the philosophy of total process management. Language primitives can make any number of scheduling requests; the kernel is responsible for throttling parallelism to avoid the danger of excessive parallelism.
DSI's approach to controlling parallelism is based on our load-sensitive distributed allocation policy outlined in section 5.2.2. Since suspensions only execute locally, the load-sensitive allocation automatically limits the number of new processes created on a given processor by other processors. This in turn limits the possible number of scheduling requests made to a processor by other processors for those suspensions. Thus the only unlimited parallelism that a processor needs to worry about comes from local scheduling requests; i.e. made by local processes. This suggests a two-tiered approach for differentiating between local and remote scheduling requests. Each processor maintains one queue for incoming remote scheduling requests and a separate area for local scheduling requests. The two structures have distinct scheduling priorities. If a processor always favors its incoming scheduling queue (requests from other processors to execute local suspensions) then it automatically favors the status quo of current parallelism load on the machine, and thus discourages parallel expansion occurring from its local scheduling area. The allocation block size and allocation server responsiveness (see sections 5.2.1 and 5.2.2) indirectly determine the current load for the reasons outlined above. These factors affect the number of possible outstanding remote requests for a processor's local suspensions, thus controlling the backlog of multiple outstanding dependence stacks.
If there are no outstanding scheduling requests in a processor's incoming queue it obtains a scheduling request (dependence stack) from the local area. If this process should probe a remote suspension, it will be blocked on the dependence stack and a scheduling request will be sent to the remote processor. Note that this effectively raises the blocked task into a higher priority level, since it will be rescheduled in the sending processor's incoming queue after the probed suspension converges on the remote processor. Thus the absence of work in a processor's incoming queue results in that processor augmenting the level of parallelism in the overall system by expanding tasks in its local area.
The type of parallel expansion occurring in this way depends on whether we use a stack or a queue for the local scheduling area. A queue results in a breadth-first expansion; a stack results in a depth-first expansion. Superficially, a queue might seem to be the better choice. Breadth-first expansion expresses parallelism at higher levels in the process decomposition, which is generally preferable. Depth-first expansion limits the exponential growth of parallel decomposition. Note, however, that parallel expansion due to our distributed allocation/load-balancing scheme also affords breadth-first parallelism6.2, and in fact, this is exactly the mechanism that is used to distribute parallelism evenly. Our remote queue represents the desired parallelism load; our local scheduling area is excess parallelism. With this in mind, we choose a LIFO approach for the local scheduling queue, which further throttles parallel expansion.
The priorities of the incoming queue and stack are easily handled by DSI's signal mechanism; these structures are implemented by the prioritized interprocessor message queues described in section 4.3. This mechanism insures a timely interruption of the processor should a remote scheduling request become available.
In contrast to conservative parallelism is speculative
parallelism [Jon87] (also called speculative
computation [Osb90]).
The results of speculative processes are not known to be
needed.
Speculative processes are usually scheduled based on some
probability of need.
For example, consider a speculative conditional
that schedules its then-part and else-part in parallel
with the evaluation of the predicate, on the idea that
it will make some headway on the result regardless of the outcome of
the test.
There are a number of useful applications of speculative computation;
section 2.3 contains several examples.
Osborne [Osb90] provides a partial taxonomy for
classifying speculative computation types.
The first problem, that conservative processes take priority over speculative processes, is easily satisfied by having each processor maintain a separate, lower priority queue for speculative processes. If a speculative process probes or schedules any other suspensions they are also scheduled to the appropriate processor's speculative queue. Thus, once a task has been scheduled speculatively, neither it nor any of its descendants should be scheduled to a conservative queue. At first, this approach does not seem to provide for contagion [Osb90]; namely, if sharing relationships are such that a conservative process comes to depend on a speculative task (e.g. by probing it after it has been scheduled speculatively elsewhere, like our speculative conditional) the speculative process should be upgraded to conservative, and any tasks it depends on should be upgraded as well. We will address this issue in our discussion on sharing in section 6.8.
Our second concern, that speculative parallelism be controlled, is satisfied by the same techniques we used in controlling conservative parallelism: using a stack to schedule local suspensions. Since we are segregating speculative and conservative processes, we add a local, speculative stack in addition to our speculative queue described above. The stack works in exactly the same way as the conservative stack described in section 6.6; local speculative suspensions are pushed on the stack, and remote speculative suspensions are appended to the speculative queue on the remote processor. The speculative stack has lower priority than the speculative queue, which favors existing parallelism over new parallelism. Thus, we have two queues and two stacks per processor, which are serviced in the following priority (highest to lowest):
Ideally, the system should spend as little effort as possible on useless task removal; any effort spent in doing so is chalked up to pure overhead that offsets any gains made in profitable speculation. The approaches used by current parallel symbolic systems generally fall into two categories: explicit killing of tasks [GP81,Hem85] and garbage collection of tasks [BH77,Mil87].
The first approach, explicit killing of tasks, relies on the kernel being able to determine when a task has become useless. At that point the kernel can spawn a termination task, which begins at the root of the speculation process subtree and recursively kills tasks. Alternatively, the kernel can cut the useless processes out of the schedule directly. This can be difficult to do if a distributed scheduling structure is used, as in DSI. Both methods require the kernel to be able to identify all descendants of the useless task and determine whether they are useless or not; because of sharing, some of them may not be useless and should be spared.
The garbage collection approach involves modifying the garbage collector to remove useless tasks from schedules, blocking queues, and other scheduling infrastructure. This approach assumes that useless tasks have become unreferenced from the computation graph. In order to keep them from being retained by scheduling references, weak pointers or weak cons cells [Mil87] must be used to build scheduling infrastructure containing pointers to tasks so that they aren't retained unnecessarily. A potential problem with this approach is that useless tasks continue to remain in the system until garbage collection [Osb90]. One way to prevent this is through the use of priorities, especially if priorities are already being used to give conservative tasks preference. When a task is discovered to be useless, priorities can be propagated down through the speculative process subgraph to downgrade the status of all descendant tasks. As with the killing approach, the kernel must be able to distinguish the useful from the useless as it descends the subtree; this may require a sophisticated priority combining scheme [Osb90].
This approach supports a number of speculative models [Osb90]. Simple precomputing speculation is accomplished by a single coax. This type of speculation simply channels some effort into executing a suspension on the chance that it's result will be needed later. Multiple-approach speculation is more common, and refers to scheduling a number of tasks where not all of them are necessary. Constructs falling into this category are our speculative if (see above), AND-parallelism, OR-parallelism, and many others (see section 2.3). These primitives operate on the principle of strobing: coaxing a number of suspensions repeatedly until one converges. This may be enough for the scheduling task to produce a result; if not, the task may resume strobing until another converges, and so on. The kernel provides routines to handle this strobing on behalf of primitives6.3 this simplifies the construction of speculative primitives, and allows the kernel to optimize the strobing behavior.
There are a number of advantages in this approach to managing speculative tasks:
In order for bounded computation to be effective, our system must be able to extend a process's bound to other processes that it probes or schedules indirectly. To do this we modify our demand-driven scheduling scheme to propagate demand coefficients and observe the limits of a process' computation bound. This essentially quantifies the demand propagating through the computation graph.
In implementation terms, this entails the transfer of coefficients along the fringe of the computation; i.e. at the top of the process dependence chains. When a dependence stack is extended, the kernel transfers some or all of the scheduling process' coefficient to the target suspension. If the target process converges, the kernel transfers the remaining portion of the coefficient back to the process being resumed. If a process exhausts its coefficient before converging, the kernel unwinds the dependence stack until it discovers a suspension with a positive demand coefficient, and schedules it on the owning processor.
The size and transfer characteristics of demand coefficients must be carefully determined, in much the same way as allocation blocksize is for distributed memory allocation. If set too small, then coaxed computation does not get very far, per coax, and coaxing overhead begins to overtake speculative processing; If set too large, useless tasks will remain in the system for longer periods, although they only compete with other speculative tasks. A strict requirement for the transfer function is that coefficients should monotonically decrease over the course of several transfers; otherwise a chain of speculative demand might live on indefinitely.
The problem with speculative processes points out how dependences are a temporal phenomenon, which is the reason it is problematic for the system to accurately dynamically track the dependence relationships between processes. There are other reasons besides speculation that might result in a dependence changing without the system's awareness. For example, a suspension might be moved to a new location by another process, or a location containing a suspension might be overwritten by another process6.4. Therefore it is somewhat of a philosophical decision not to embed temporal dependence information in suspensions themselves, since it may later prove inaccurate. The actual state of dependences is recorded in the suspension state already, in the form of their actual pointer values and code that they are executing. Thus the truest form of demand-driven scheduling would be to poll repeatedly from the root of the entire computation tree, allowing the dependences to ``shake out'' naturally. Unfortunately, this approach is not feasible on stock hardware, and would result in many suspensions being swapped in repeatedly only to block on their dependences and be swapped out again. DSI's current approach using dependence stacks is a compromise; it prevents the most common form of polling inefficiency, while still providing a method (demand coefficients) for utilizing the programs actual dependences to handle speculation.
One way to increase process granularity is by replacing invocations of suspend (especially for trivial suspensions) to inlined code or recursive function calls where appropriate. This helps, but not overly so because of the high level of optimization already performed for suspension processing. Informal tests indicate that a function call is only slightly faster than locally coercing a suspension. How much faster depends on how many registers need to be saved on the stack to perform a strict function call; because suspensions are so small, a context switch can be faster than a function call that has to perform several allocations to save and restore registers. Also, many suspensions cannot be eliminated or inlined and still retain proper laziness. Compilation, including strictness and dependence analysis can help to improve granularity. Demand coefficients may also provide a way to implement bounded eagerness; this idea is explored further in chapter 8.