This is an
OpenGL-based course introducing the mathematical foundations and practical
programming methods of modern interactive computer graphics. The homework
involves coding in C using OpenGL and GLUT, and mastering the
theoretical principles upon which OpenGL-like graphics is based.
The course emphasizes creating interactive interfaces to help understand
the graphics objects and techniques being studied. Lighting and
simple material modeling are covered as an introduction to the
creation of realistic images.
This course focused on Mathematica-based methods of
producing rapid prototypes solving complex software modeling problems.
This class will start with an introduction to the Mathematica
programming environment, and will incorporate Mathematica prototyping
methods implicitly into a broad survey of mathematical modeling methods,
techniques, and folklore used widely throughout computer science,
computer graphics, scientific visualization, mathematics, and physics.
- Images of Mathematical Physics: Calabi-Yau
spaces
Shown below are my graphical representations of the
Calabi-Yau quintic representing the hidden dimensions of string
theory, based
on my 1994 paper. These were made available on the
Wiki Commons domain in 2014, and clicking on the images takes you to
the source material. The first is a 2-dimensional cross-section of
the quintic in CP2, and the second is a complete
6-dimensional representation of the (local C4) quintic
embedded in CP4 using 4D discrete samples in a
C2 subspace to produce a hypercubic array of the
corresponding varying 2D cross-sections.
|
- Mathematical Physics and Astronomy:
| Charting the Interstellar Magnetic Field behind the {\it Interstellar
Boundary Explorer {(IBEX)}} ribbon of Energetic Neutral Atoms
,
by P.C. Frisch, A. Berdyugin, V. Piirola, A.M. Magalhaes,
D.B. Seriacopi, S.J. Wiktorowicz, B-G Andersson, H.O. Funsten,
D.J. McComas, N.A. Schwadron, J.D. Slavin, A.J. Hanson, and
C.-W. Fu, appearing in
Astrophysical
Journal, November, 2015. A local copy can be found
here.
|
| [DQT2] Discrete Quantum Theories,
by Andrew J. Hanson, Gerardo Ortiz, Amr Sabry, and Yu-Tsung Tai,
appearing in
J. Phys. A: Math. Theor. 47 (2014) 115305 (20pp) (March,
2014). This work continues a systematic investigation of the
formulation of discrete quantum computing using finite fields, and
introduces that concept of Cardinal Probability as a way of
dealing with probabilistic concepts in the absence of ordered
numbers for finite fields. The DOI link is
doi:10.1088/1751-8113/47/11/115305.
A local copy can be found
here.
|
| [DQT1]
Geometry of Discrete Quantum Computing,
by Andrew J. Hanson, Gerardo Ortiz, Amr Sabry, and Yu-Tsung Tai,
appearing in J. Phys. A:
Math. Theor. 46, no. 18, pp. 185301 (22 pages), (2013).
The DOI link is
doi:10.1088/1751-8113/46/18/185301,
This work presents the mathematical elements of the consequences of
formulating quantum computation and qubits in terms of discrete,
computable numbers, using complexifiable fields with finite
characteristic.
A local copy can be found
here.
|
- Interfaces and Visualization:
| Scheduling Scaffolding: The Extent and
Arrangement of Assistance During Training Impacts Test Performance,
by Jonathan G. Tullis, Robert L. Goldstone, and
Andrew J. Hanson, appearing in the
Journal of Motor Behavior, pp 01--11, (2015)
The DOI is
DOI:10.1080/00222895.2015.1008686.
|
| Putting Science First: Distinguishing Visualizations from
Pretty Pictures.
Andrew J. Hanson,
"Putting Science First: Distinguishing Visualizations from
Pretty Pictures," in
Visualization Viewpoints column, Theresa-Marie Rhyne,
editor. IEEE Computer Graphics and Applications, Vol 34, No. 4,
pages 63--69, (July/August 2014). A local copy is
here.
|
| Interactive Exploration of 4D Geometry with Volumetric
Halos
Weiming Wang, Xiaoqi Yan, Chi-Wing Fu, Andrew J. Hanson,
and Pheng-Ann Heng.
``Interactive Exploration of 4D Geometry with Volumetric Halos.''
In Proceedings of Pacific Graphics 2013
(Singapore, October 7--9, 2013).
The DOI link is
DOI:10.2312/PE.PG.PG2013short.001-006.
A local copy
is here.
|
| Multitouching the Fourth Dimension.
By Xiaoqi Yan, Chi-Wing Fu, and Andrew J. Hanson,
IEEE Computer, Volume 45, Number 9, pp.80-88 (September,
2012).
IEEE site for PDF:
is here.
|
- Genomics, Proteomics, and Quaternion Maps:
| Localization of polymerase IV in Escherichia coli
By Sarita Mallik, Ellen M. Popodi, Andrew J. Hanson, and Patricia
L. Foster.
"Interactions and localization of Escherichia coli error-prone DNA
polymerase IV after DNA damage," J. Bacteriol. (June 2015).
Accepted manuscript posted online 22 June 2015.
DOI link is here
doi:10.1128/JB.00101-15,
Abstract is here, and the pre-publication
manuscript is here.
|
| Mutational Topology of the Bacterial Genome.
By Patricia L. Foster, Andrew J. Hanson, Heewook
Lee, Ellen Popodi, and Haixu Tang. "On the Mutational Topology of
the Bacterial Genome," G3: Genes, Genomes, Genetics,
Volume 3, no. 3, pp. 399--407 (March 2013).
Pub Med link:
is here,
DOI link is
here,
and the Journal URL
link
is here.
|
| "Quaternion maps of global protein
structure,"
By A.J. Hanson and S. Thakur, appearing in
Journal of Molecular Graphics and Modelling, Volume 38,
September 2012, pp. 256--278.
The paper PDF site is here.
|
- Presentations and Talks:
| Talk. Discrete Quantum
Computing,
Andrew J. Hanson
(with Gerardo Ortiz, Amr Sabry, and Yu-Tsung Tai),
Seminar for Quantum Computing Group, Computer Science, Oxford University,
Oxford, UK (25 July, 2014).
|
| Talk. The Bugcatcher.
Andrew J. Hanson
(with Jonathan Tullis and Rob Goldstone),
``The Bugcatcher,'' 25 June, 2014.
ASIC 2014 (23--27 June 2014, Moab, Utah).
|
| Talk. Multitouching the Fourth
Dimension.
Andrew J. Hanson, ``Multitouching the Fourth
Dimension,'' ASIC 2013 (24--30 July 2013, Cortina d'Ampezzo, Italy).
|
| Course. Quaternion
Applications.
Andrew J. Hanson: Presented at Siggraph Asia (Singapore, 29 November, 2012).
New application topics included optimal,
smoothly controllable tubing and tube texturing, quaternion protein
maps, and how dual quaternions solve the century-old conundrum of how a
quaternion acts on a vector.
|
Interactive Mathematics
|
Click here for a larger version
|
4Dice is my (free) iPhone App.
See our
IEEE COMPUTER paper
(pdf link:
here)
on the design of 4Dice,
IEEE Computer, Volume 45, Number 9, pp.80-88 (September,
2012).
Alternative site for PDF:
see also here.
4Dice is an interactive application using our
4D Rolling Ball algorithm combined with the
graphically correct
4D backface-culled
representation of the hypercube introduced in the 4Dice
video animation (see below). This is a collaborative project
with Xiaoqi Yan and
Prof. Philip Chi-Wing Fu at NTU, Singapore.
The
4Dice one-minute YouTube video provides a quick introduction
to the issues of properly visualizing a back-face culled hypercube;
the 4Dice iPhone App provides interactive exploration of all
the concepts introduced in the animation.
|
Make a Hypercube in Lights
|
|
|
|
|
|
|
The images you see in the 4Dice interactive application
actually form a wire-frame torus when you turn off back-face
culling. The deep reason for this is that the hypercube is a simple
tessellation of a 3-sphere (which has Euler characteristic zero)
surrounding a 4-ball, and a nice parameterization of the 3-sphere
involves a nested family of tori; the wireframe hypercube is
effectively a rectangular tessellation of the "center"
member of this family of tori. It is known that such a set of
edges, with four edges meeting at each vertex, admits
an Eulerian
path. The figure on the left shows one of many such paths
that can be constructed, with a ratio of 1:3 for the inner cube edge
relative to the outer cube edge, and diagonal edges with relative
length sqrt(3). With a little work, one can use this
diagram to construct a hypercube out of a single string of holiday
lights, as shown on the right.
(With a tip of the hat to Priscilla and
Russell.)
|
Selected Publications of Interest
|
Visualizing Quaternions
(Morgan-Kaufmann/Elsevier, 2006, ISBN 978-0-12-088400-1)
is a comprehensive approach to the
significance and applications of quaternions,
and focuses on the exploitation of Quaternion Fields,
a tool developed primarily by the author.
The
official website for the book is maintained by the publisher,
and provides background material, downloadable material from tables,
and demonstration software.
I maintain a local
companion website here, which may be more up to date.
Updates and Errata are maintained on the update
and errata page.
An example is the closed form double-reflection quaternion form
q = ( A · B, A × B ) inadvertantly
omitted from the Clifford Algebra treatment in Chapter 31.
There are several array indices that are transposed in
the C Program in Table E.3, page 446.
|
|
|
Winner with co-author Sidharth Thakur of the
2012 JMGM Graphics Prize.
See also the
MGMS/Elsevier Graphics Award.
Quaternion Approaches to Visualizing Protein Structure are
worked out in detail in
our JMGM article:
A.J. Hanson and S. Thakur, "Quaternion maps of global protein structure,"
Journal of Molecular Graphics and Modelling, Volume 38,
September 2012, pp. 256--278.
(Alternate URL here.)
Quaternion maps of protein amino acid residues provide an
alternative to Ramachandran plots for orientation analysis. Several
alternative orientation frame systems can be chosen, with the
residue-local Cα-centered frame being the default. Quaternion
maps are noteworthy for their ability to compare the orientations of
arbitrary sets of sequential or non-sequential residues located
anywhere on the protein, and for the resulting opportunity to observe
and analyze the statistical properties of global orientation clusters.
Only the quaternion representation of orientation frames embodies a
natural rigorous measure for comparing properties of sets of global
orientation frames.
|
| |
Quaternion Applications were covered in our updated
quaternion tutorial lectures presented at Siggraph Asia 2012, 29
November in
Singapore. Special application topics included
optimal, smoothly controllable tubing and tube texturing,
quaternion protein maps, and how dual quaternions solve the
conundrum of how a quaternion acts on a vector. The latter is a
long-standing controversy that pitted Hamilton against many
contemporaries, and has been described in wondrous detail by
Altmann in
"Hamilton, Rodrigues, and the Quaternion Scandal.";
The solution is simply to replace Hamilton's impossible candidate for
a "Vector," the binary rotation quaternion (0,
(x, y, z) )
by the dual quaternion vector, namely (0,
ε(x, y, z) ), with
ε having the dimension of inverse length and
satisfying ε2 = 0 .
Visualizing Relativity using complexified quaternions was
part of the material covered by Andrew Hanson and
Daniel Weiskopf in their
Siggraph 2001 Course 15 Notes.
The Solar Journey DVD
contains an educational computer animated film on the astronomy
of the local neighborhood of the Earth and the Sun developed as
part of our NASA-sponsored research work. The DVD version containing
the Solar Journey animation and supplementary science materials
is distributed by
Finley-Holiday Films.
|
BIBLIOGRAPHY, HISTORICAL WORKS, and MEDIA:
Some day I'll put together an annotated bibliography, but for
now see the Google Scholar and DBLP project links at the top
of the web page. Here is a summary of my historically most highly
cited work, and together with some media links.
The Eguchi-Hanson
metric (Physics Letters 74B, pp. 249--251 (1978)) is a
vacuum solution of
the Euclidean Einstein equations that is the first known instance of
an important class of metrics now commonly referred to as ALE
or Asymptotically Locally Euclidean metrics. A comprehensive
review of Euclidean Einstein metrics and the context of the
Eguchi-Hanson metric is given in
our 1979 Annals of Physics review article. This work
won the Second Prize in the 1979 Gravity Research Foundation
Competition; see
T. Eguchi and A.J.Hanson,
"Gravitational Instantons,"
Journal of General Relativity and Gravitation,
11, pp. 315--320 (1979).
Our comprehensive introduction
to the ways in which the languages of the theoretical physics and
mathematics communities became inseparably connected after a long
history of going their separate ways is available in the
1980 Physics Reports article
"Gravitation, Gauge Theories and Differential
Geometry" by Eguchi, Gilkey, and Hanson.
Constrained Hamiltonian Systems, is a short book by Hanson, Regge,
and Teitelboim, originally published in 1976 by the Accademia
Nazionale dei Lincei (Contributi del Centro Linceo Interdisc. di
Scienze Matem. e loro Applic., No.22, Accademia Nazionale dei Lincei,
Rome, 135 pages (1976)). Actual print copies of this work are rare
and generally unavailable.
Media.
The four-dimensional MeshView viewer is described in the
Meshview tech note, and downloadable software is located
HERE. Supported fully under X-windows/Motif only.
Precompiled for Linux, Macintosh, SUN SOLARIS, and SGI IRIX.
Recently available:
reduced functionality Windows XP version. The shortcuts work
in the Windows version, but you need to look at the Linux version
to see what they are.
Some Recent Research Topics
My research in the recent past has focused on several areas,
including: Mathematical
Visualization, Virtual Reality, and Astronomy.
- Mathematical Visualization:
| A Tessellation for Fermat Surfaces in CP3,
DOI link
10.1016/j.jsc.2008.09.002, appears in the Journal of Symbolic Computation
(Sept 2008). This work presents an explicit algorithm for tessellating
the algebraic surfaces (real 4-manifolds) F(n) embedded in
CP3 defined
by the "Fermat" equation
z0n + z1n + z2n + z3n
= 0
in the standard homogeneous
coordinates [z0, z1, z2, z3], where n is any positive integer. Note
that F(4) in particular is a K3 surface. Thus this method provides
what is essentially an elegant 24-point tessellation of K3.
The outdated original arXiv posting is here: 0804.3218.
A local copy can be found
here.
|
| Dual Five-Point Function Geometry.
This work investigates the geometry of two-complex-variable
contour integration using the classic 1960's Dual 5-Point Function of
the early string model as the critical example. The investigation
actually began with some questions introduced in a very early
paper, Dual N-Point Functions in
PGL(N-2,C)-Invariant Formalism (A. J. Hanson, Physical Review, 1972).
A number of new insights are given in our paper
"A Contour Integral Representation for the Dual
Five-Point Function and a
Symmetry of the Genus Four Surface in R6" by Andrew
J. Hanson and Ji-Ping Sha, DOI link
10.1088/0305-4470/39/10/01,
which is published in
J. Phys. A: Mathematics and General.,
vol. 39, pages 2509-2537 (2006). There is also a version
on the arXiv, math-ph/0510064.
A local copy can be found here.
|
Other topics. Various long-term projects deal
with techniques for modeling, depicting, and interacting with geometric structures
of extreme complexity. Subject domains of interest range from mathematical
objects in four dimensions to exploiting quaternions to represent orientation
fields of geometric objects. Recent work concerns rephrasing some of the
classical differential geometry of curves and surfaces directly in terms
of quaternion fields; an application is the determination of optimal framings
of curves and surfaces by minimizing appropriate energies of the quaternion
frame fields ("quaternion Gauss maps") in the 3-sphere.
- Constrained Navigation Approach to User Interfaces for Virtual Reality Applications:
Work with Eric Wernert on constrained navigation methods for desktop and
immersive Virtual Reality systems appear in the Proceedings of IEEE
Visualization '97 and '99. Browse our Vis97 paper
and our Vis99
paper.
- Scientific Visualization in Astronomy: The Solar Journey
project was undertaken with NASA support (NAG5-8163, NAG5-11999) in
collaboration with the University of Chicago beginning in 1999.
This has led to a number of projects
in virtual astronomy. See the
Project Data site
for examples of packages
supported under this program, including the Solar Journey package.
(Note that the AISRP Code and Algorithm Library that used to
be at " http://aisrp.nasa.gov/cal/SessionDriver/Packages/ "
has been abandoned and decomissioned by NASA for some unknown reason.)
An example of our work on star rendering embedded in the
Solar Journey package may be
found in this QuickTime movie depicting simulated
stars, which compares favorably
to real images such as Akira Fujii's
Orion.
Selected papers of ours in this area:
|
Visualizing Multiwavelength Astrophysical Data,
Hongwei Li, Chi-Wing Fu, and Andrew J. Hanson,
TVCG, Nov/Dec 2008, 14, no. 6, pp. 1555-1562,
Proceedings of IEEE Visualization 2008. Describes
a unique interactive GPU-driven volume-rendering
paradigm tailored to the study of all-sky multispectral astrophysical
data.
Paper web site.
|
|
Visualizing Large-Scale Uncertainty in Astrophysical Data,
Hongwei Li, Chi-Wing Fu, Yinggang Li, and Andrew J. Hanson,
TVCG, Nov/Dec 2007, 13, no. 6, pp. 1540-1647;
Proceedings of IEEE Visualization 2007. Astrophysical data
is characterized by a wide variety of uncertainties and error sources;
this work provides a set of tools for examining and visualizing these
features.
Paper
and web site.
|
|
A Transparently Scalable Visualization Architecture for Exploring
the Universe, TVCG, Jan/Feb 2007, is a full
description of work done mainly by Chi-Wing Fu in my laboratory. This
framework supports
transparent interactive navigation across enormous scale ranges
such as those naturally occurring in astronomy.
Paper and web site. |
|
Scalable WIM: Effective Exploration in Large-scale Astrophysical
Environments, TVCG, Sept/Oct 2006, 12, pp. 1005-1011;
Proceedings of IEEE Visualization 2006.
Describes a World-in-Miniature interface design for astrophysical
exploration whose development was led by Yinggang Li in my laboratory.
Paper and web
site. |
|
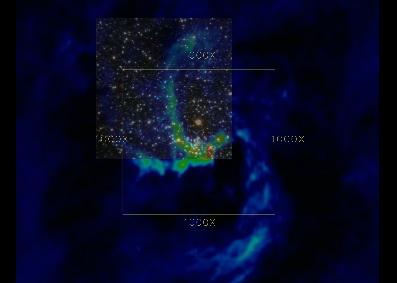
Approach to the Black Hole at the Galactic Core.
This animation represents an assembly of data collected by
astronomers all over the world to examine the surroundings
of the Black Hole suspected to be present at the center of
our Milky Way galaxy. A variety of scientific instruments,
using different methods and different wavelengths have
been utilized to get many orders of magnitude of image precision.
This permits us to make a continuous fly-in starting from the familiar
constellations and going all the way in
to the stars actually orbiting the Black Hole itself.
|
|
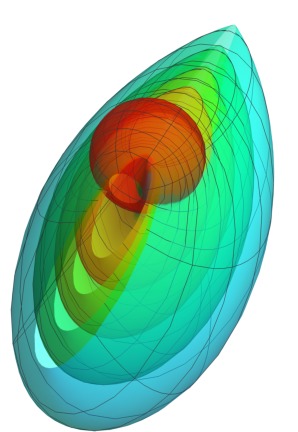
The Sun's interaction with its environment.
This image of the heliosphere, representing the interaction
of the Solar wind with the surrounding interstellar material,
is taken from our short film "Solar Journey;" an extended
version of the film will be produced for public distribution on
videotape and DVD during the coming year. The
shapes depicted here utilize a theoretical model by Timur Linde from
the University of Chicago. The image has appeared as the Astronomy Picture
of the Day,
APOD 2002 June 24,
and was used as an illustration in a recent astronomy
news article in Science Magazine, page 2005 of
Vol. 300, 27 June 2003. (The image credit is very obscure, in tiny
vertically-aligned print along the spine of page 2005.)
|
|
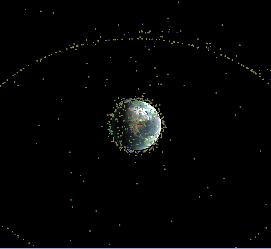
Satellites in our Sky (GMT June 24th 2003 2:21pm).
We have over a thousand satellites flying through the sky over our
heads. This image is from a
brief animation representing a user's interaction with
our Earthday graphics program. The animation
shows a large portion of these at a
selected time, and then zooms in for a closeup of the International
Space station (ISS).
We can clearly see the ring structure of geo-stationary (deep-space) satellites
rotating with the Earth, located 38,500km
above the Earth's surface (about 6 times the radius of the Earth).
The entire animation appeared as the Astronomy Picture
of the Day on 14 July 2003. See
APOD 2003 July 14.
|
Our initial work on handling very large scales of spacetime
in interactive virtual reality environments is described in our paper, Very large
scale visualization methods for astrophysical data, which appears in
Proceedings of Joint Eurographics-IEEE TVCG Symposium on Visualization,
May 29-31, 2000, Amsterdam, the Netherlands. This paper is part of the
published proceedings, © Springer-Verlag.
Our most extensive recent work, which appeared in TVCG in January 2007, describes the
maturation of the scaling framework developed in Philip Chi-Wing Fu's
PhD thesis, and is entitled "A Transparently Scalable
Visualization Architecture for Exploring the Universe."
For details, see the
summary web site.
Calabi-Yau Cross Sections:
I have also created a variety of graphics images derived from the Fermat
Equation (see below) that are relevant to the Calabi-Yau spaces that may
lie at the smallest scales of the unseen dimensions in String Theory; these
have appeared in Brian Greene's books, The Elegant Universe
and The Fabric of the Cosmos,, and
in the book by Callender and Huggins, Physics
Meets Philosophy at the Planck Scale. The writhing purple shapes
in the October/ November 2003 NOVA production Elegant Universe,
as well as the cover of the November 2003 Scientific American,
were derived from software models I supplied to the NOVA graphics
providers.
These images show equivalent renderings of a 2D cross-section of the
6D manifold embedded in CP4 described in string theory calculations by the
homogeneous equation in five complex variables:
z05 + z15 +
z25 + z35 +
z45 = 0
The surface is computed by assuming that some pair of complex inhomogenous
variables, say z3/z0 and z4/z0, are constant (thus defining
a 2-manifold slice of the 6-manifold), normalizing the resulting inhomogeneous
equations a second time, and plotting the solutions to
z15 + z25 = 1
The resulting surface is embedded in 4D and projected to 3D using Mathematica
(left image) and our own interactive MeshView 4D viewer (right image). If
you have
CosmoPlayer, you can also
interact with this VRML version
of the quintic Calabi-Yau cross-section.
In the right-hand image, each point on the surface where five different-colored
patches come together is a fixed point of a complex phase transformation;
the colors are weighted by the amount of the phase displacement in z1 (red)
and in z2 (green) from the fundamental domain, which is drawn in blue and
is partially visible in the background. Thus the fact that there are five
regions fanning out from each fixed point clearly emphasizes the quintic
nature of this surface.
For further information, see: A.J. Hanson.
A construction for
computer visualization of certain complex curves.
Notices of the Amer. Math. Soc., 41(9):1156-1163, November/December
1994.
An interactive version is available at
the Wolfram Demonstrations Project Calabi-Yau
Space page, based on the Hanson paper cited above, with
assistance from Jeff Bryant.
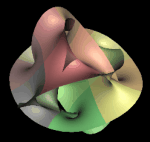
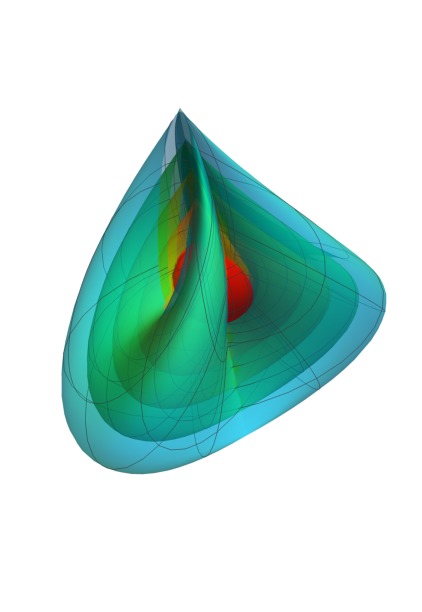
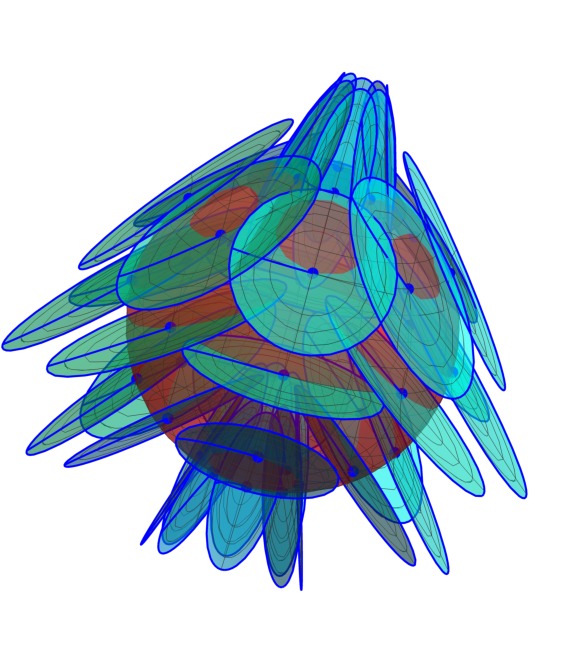
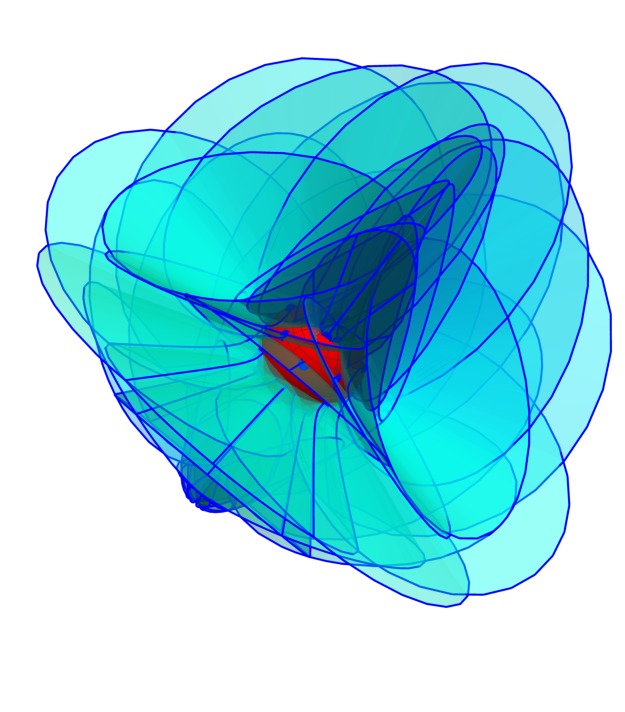
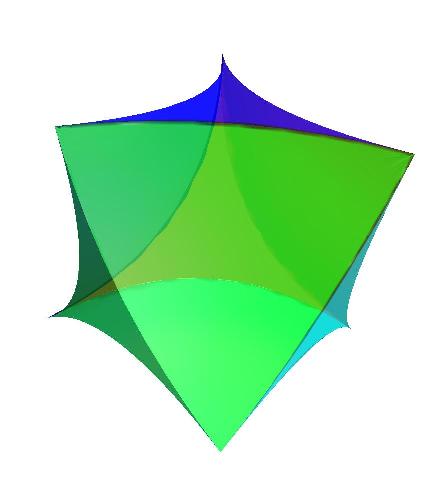
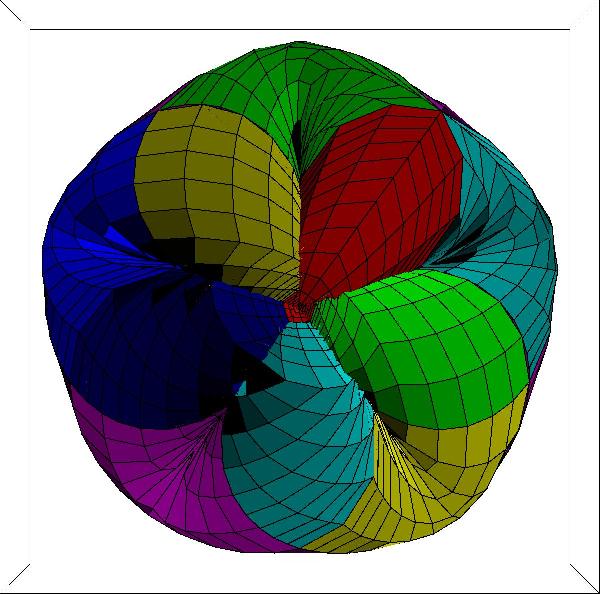
Arbitrary Genus Surfaces:
This image shows my computer graphics construction of a four-hole
torus described by an equation in complex two-space given by H. Blaine
Lawson, "Complete Minimal Surfaces in S3," Ann. of Math. 92,
pp.~335--374 (1970), with m = n = 2,
Im z1(m + 1) + |z2|(m-n) Im z2(n+1)
= 0
and
|z1|2 + |z2|2 = 1
In general,
the genus is m*n, and this surface is not actually minimal in S3
except for
m = n = 0 and m = n = 1.
Review article
Cover picture: IEEE Computer 27 (July 1994)
- For more information about mathematical visualization in general,
see the Web version of the review article
Interactive Methods for Visualizable Geometry, by A.J. Hanson, T.
Munzner, and G. Francis, published in IEEE Computer 27 ,
No. 7, pp. 73--83 (IEEE Computer Society Press, Los Alamitos, CA, July,
1994).
Mathematics and Physics Animations
We have produced a number of short video animations with mathematical and
physical content. Some of my favorite projects are the following:
- Cosmic Clock:
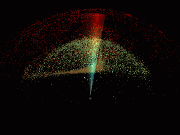
Observing the Universe using the finite speed of light to place measured
objects in their correct temporal context.
- The Cosmic
Bloom excerpt from the movie as available here; it seems to play OK on
PC's with QuickTime, but has troubles on some other platforms.
- This 3:35 minute animation contains a visualization of the entire
Universe from three different points of view: the time spectrum of observable
photon radiation arriving at the earth, the constant-time shells of light
sources represented in "comoving coordinates " (as though the Universe
had always been the size it is today), and in "physical coordinates" (which
incorporate the Hubble expansion since the "Great Flash", when the Universe
was about 300,000 years old). This film was one of a select few chosen for
showing at the Siggraph 2000 Electronic Theater in July 2000, and appears
in Siggraph Video Review 134, Scene 5 (2000).
-
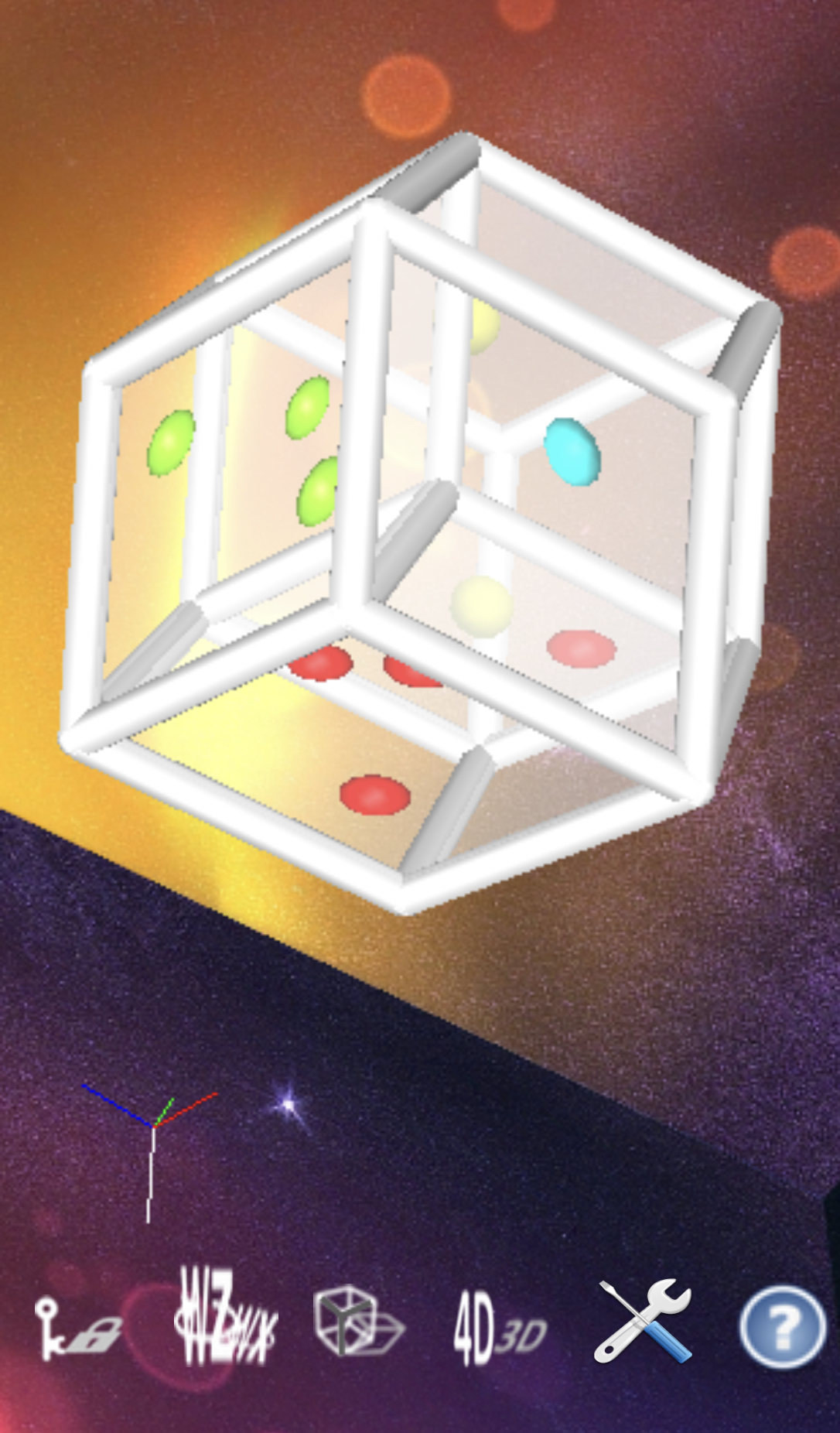
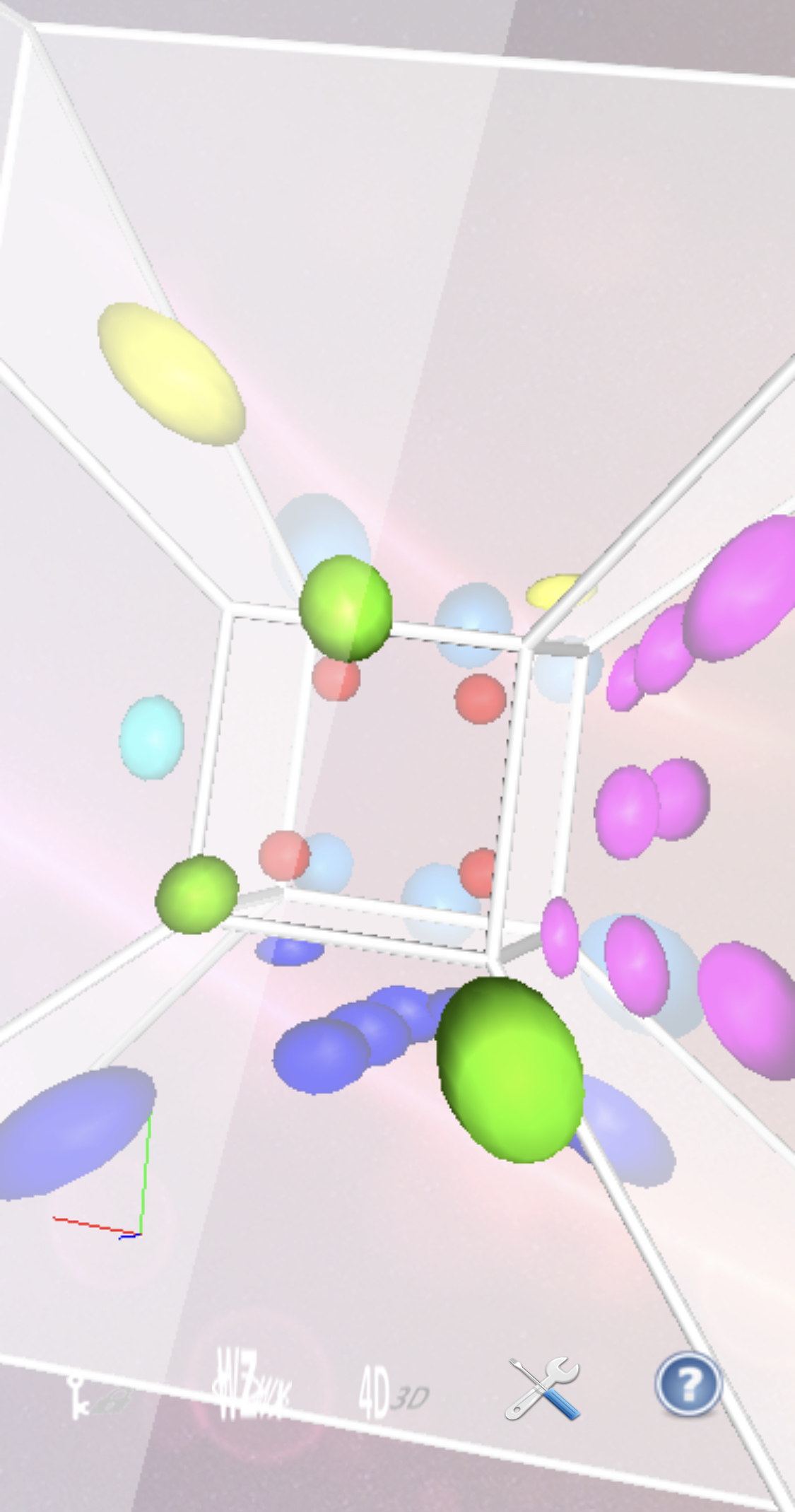
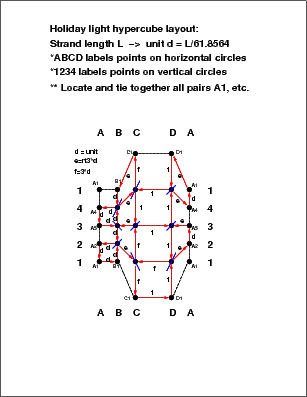
4Dice: Hypercube
4Dice: A Glimpse into the 4th Dimension (MPG silent version)
-
4Dice: Local version with narration.
-
4Dice: YouTube version
with narration.
- This short (1:00 minute) animation of a back-face-culled 4D die or
hypercube, which has eight sphere-containing cubes as the analogs of faces,
was shown at the Siggraph '95 Computer Animation Festival and appears in
Siggraph Video Review 114, Scene 14 (1995).
- Visualizing Fermat's Last Theorem:
Visualizing Fermat's Last Theorem Video
-
Fermat Video YouTube version:
- Fermat's last theorem was proven at last in 1995 by Andrew Wiles, but
the mystique lives on. This film was made in 1990, when it was still unclear
that Fermat's conjecture would ever actually be proven --- in a way it was
more romantic when we could believe that, wasn't it?
- The film was shown in the Siggraph '90 Animation Screening Room,
and appears in Siggraph Video Review 61, Scene 4 (1990).
Andrew J. Hanson: Last revised 22 April 2015.
