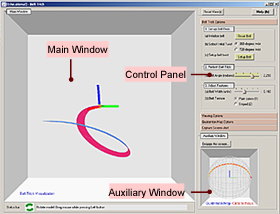
1. Introduction:
The 'Belt-Trick' visualizes the nature of
the group of rotations (or the Group SO(3)) in
three-dimensional space. One of the unique and interesting
properties of this group is that a belt with two twists and fixed
ends can be continuously deformed into a straight and untwisted
belt. The same, however, is not true for a belt with only one twist.
This striking phenomena can be demonstrated by
using any ordinary belt. However, the physical demonstration lacks
sufficient information which is necessary to completely characterize
the behavior of the belt. This shortcoming of the physical
demonstration is overcome by using graphical visualization of the
phenomena. The visualization allows not only the manipulation of the
belt-deformation, but also displays the relevant information from a
unique perspective that is entirely missing in the physical
counterpart of the trick.
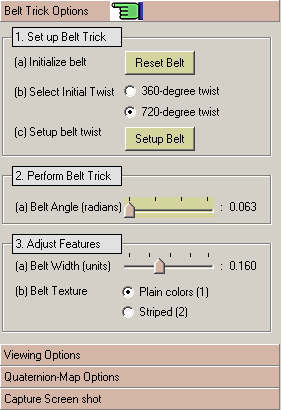
2. Using Quaternions to Describe Belt-Trick:
The unique perspective is provided by employing
Quaternions to visualize the intriguing phenomena of the
belt-trick. Quaternions are vectors in four-dimensional Euclidean
space (R4) and unit-quaternions represent
orientations in the lower, three-dimensional space. An orientation
can be thought of as a triad of three, mutually perpendicular axes,
with one axis along the fixed axis of rotation.
Quaternions are used in this manner to represent
orientations of the segments on the belt, which lie adjacent to one
another along the length of the belt. Since quaternions are
four-dimensional vectors (think quaternion, q = (w, x, y, z), where
w, x, y, z ε R, real-numbers), they are visualized by
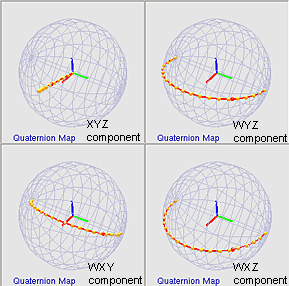
projecting the three out-of-the-four components of each quaternion
into the three-dimensional subspace. A visualization of the
quaternions is called the quaternion-map (more on
quaternion-map here).
Once each segment-orientation has been captured
by a corresponding quaternion, the series of quaternions are
connected to obtain a connected curve in the four-dimensional space,
which we call the quaternion-curve. The behavior of this
quaternion-curve, during belt deformation, then provides an insight
into why only a doubly-twisted belt straightens out.
3. Properties of Quaternion-Curve:
The quaternions for the belt-segments are
displayed as beads on the continuous quaternion-curve. Each bead
corresponds to the orientation of a single belt-segment.
Interestingly, the correspondence between quaternions and
orientations in three-dimensional space is a 2:1 mapping.
This mapping implies that each orientation in the three-dimensional
space is represented by two quaternions in the quaternion-space.
This pair of quaternions lie diametrically opposite on the unit
four-dimensional sphere (or the hyper-sphere). The two-to-one
mapping, also know as the 'double cover', has significant
implications on how a belt can deform during manipulation.
The double-cover mapping governs the nature of
the quaternion-curve for a singly-twisted (or 360°)
and a doubly-twisted (or 720°) belt. In the case
of a single or 360°-twist, the quaternion curve is
an open curve. Since the ends of the belt are fixed and not allowed
to move during the belt-deformations, the corresponding quaternions
always remain at the opposite poles on the four-dimensional sphere.
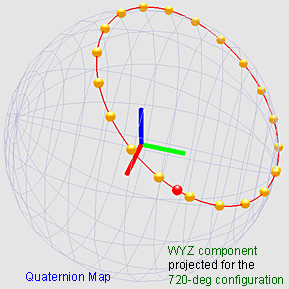
For a double or 720°-twist, the quaternion-curve
forms a loop and quaternions corresponding to the end segments are
identical.
After the belt ends are fixed and the
intermediate segments are moved in space, the quaternion-curve also
undergoes a deformation. It is observed that in the case of 360°-twist,
the quaternion-curve flips from one hemisphere of the hyper-sphere
to another. Consequently, only the direction of the twist in the
belt changes and it still remains twisted. See the snapshots
below.
On the other hand, for the 720°-twist,
the quaternion-curve continuously shrinks until it collapses into a
single quaternion. This implies that all the quaternions on the
quaternion-curve become identical and therefore all the orientations
of the belt-segments become the same. Consequently, the belt is
returned to its initial untwisted state. See the snapshots
below.