


Next: Unpredictable
Up: Randomness Assessments
Previous: Randomness Assessments
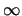 -distributed
-distributed
This definition of randomness is discussed in [8].
Let
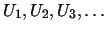 denote a sequence of uniform random variates over [0,1).
A sequence is
denote a sequence of uniform random variates over [0,1).
A sequence is 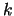 -distributed if
-distributed if
for all choices of real numbers 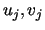 , with
, with
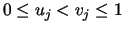 , for
all
, for
all 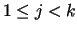 .
Put another way, each of
.
Put another way, each of 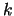 -dimensional points
-dimensional points
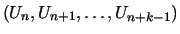 ,
,
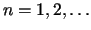 should occur the same number of times as
should occur the same number of times as 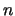 approaches
approaches 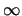 .
Note that when
.
Note that when 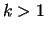 , a
, a 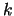 -distributed sequence is always a
-distributed sequence is always a 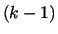 -distributed sequence
because we can set
-distributed sequence
because we can set 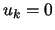 and
and 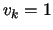 . A sequence is
. A sequence is 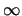 -distributed (``super-uniform'')
if it is
-distributed (``super-uniform'')
if it is 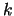 -distributed for any positive
-distributed for any positive 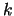 . Obviously, this definition
is only of theoretical interest and is not very useful in practice since computing resources
like space and time are finite. However, within the confines of real-world, statistical
tests like
. Obviously, this definition
is only of theoretical interest and is not very useful in practice since computing resources
like space and time are finite. However, within the confines of real-world, statistical
tests like 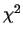 test can measure how close a finite sequence is
test can measure how close a finite sequence is 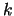 -distributed
for finite
-distributed
for finite 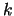 .
.
This criterion is of central importance for stochastic simulations because all numbers
in an 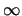 -distributed sequence are truly independent and have zero autocorrelation.
It can also be proven that such a sequence can pass most if not all existing
statistical tests.
-distributed sequence are truly independent and have zero autocorrelation.
It can also be proven that such a sequence can pass most if not all existing
statistical tests.



Next: Unpredictable
Up: Randomness Assessments
Previous: Randomness Assessments
2001-05-30
![]() -distributed sequence are truly independent and have zero autocorrelation.
It can also be proven that such a sequence can pass most if not all existing
statistical tests.
-distributed sequence are truly independent and have zero autocorrelation.
It can also be proven that such a sequence can pass most if not all existing
statistical tests.