The Interactive Activation and Competition Network: How Neural Networks Process Information

Introduction
The Interactive Activation and Competition Mechanism
The Dynamics of IAC Networks *
Back to the Jets and Sharks Network
How Neural Networks Process Information
References
Endnotes
Answers to Questions

* These sections contain some mathematics which can be omitted on a first reading if desired.

Introduction

The Interactive Activation and Competition network (IAC, McClelland 1981; McClelland & Rumelhart 1981; Rumelhart & McClelland 1982) embodies many of the properties that make neural networks useful information processing models. In this chapter, we will use the IAC network to demonstrate several of these properties including content addressability, robustness in the face of noise, generalisation across exemplars and the ability to provide plausible default values for unknown variables. The chapter begins with an example of an IAC network to allow you to see a full network in action. Then we delve into the IAC mechanism in detail creating a number of small networks to demonstrate the network dynamics. Finally, we return to the original example and show how it embodies the information processing capabilities outlined above.

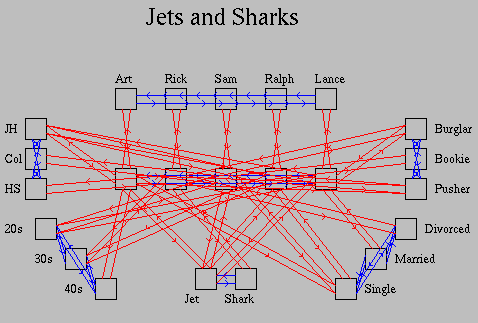
An IAC network consists of a number of competitive pools of units (see figure 1). Each unit represents some micro-hypothesis or feature. The units within each competitive pool are mutually exclusive features and are interconnected with negative weights. Between the pools positive weights indicate features or micro-hypotheses which are consistent. When the network is cycled, units connected by positive weights to active units become more active, while units connected by negative weights to active units are inhibited. The connections are, in general, bidirectional making the network interactive (i.e. the activation of one unit both influences and is influenced by the units to which it is connected).

Figure 1: The Jets and Sharks IAC network. The squares represent units and the arrows represent weights. Red arrows indicate positive weights and blue arrows represent negative weights.

The network in figure 1 represents information about two rival gangs - the Jets and Sharks (McClelland 1981). The central pool of units represent members of the two gangs. The pools around the edges represent features of these members including their name, occupation, marital status, gang membership, age and educational level. Within each pool the units are connected with negative weights indicating that they are mutually exclusive. If you are in your 20s you can't also be in your 30s, for example. Between the pools positive weights hold the specific information about each gang member. The instance unit corresponding to Art is connected to the units representing the name Art, Pusher, Single, Jet, 40's and Junior High (J.H.) - the characteristics of Art.

Table 1 shows the facts known about each of the gang members (Note: This is a subset of the full database presented in McClelland 1981).

Name	Gang	Age	Education	Marital Status	Occupation
Art	Jets	40's	J.H.	Single	Pusher
Rick	Sharks	30's	H.S.	Divorced	Burglar
Sam	Jets	20's	College	Single	Bookie
Ralph	Jets	30's	J.H.	Single	Pusher
Lance	Jets	20's	J.H.	Married	Burglar

Exercise 1: Load the network now by starting the BrainWave simulator and selecting the Jets and Sharks item from the Networks menu. Select the Toggle tool and click on the Art instance unit (in the central pool) to activate that unit. Now click on the cycle button. List the units that become active.
Exercise 2: Now click on the reset button to return all of the units to zero activation and reselect the Toggle tool. Activate the instance unit for Art and the pusher and bookie units. Now cycle. Describe what happens to the Pusher and Bookie units.

In this introductory section we have provided an overview of the IAC network. In the next section, we will examine the IAC in more detail to see exactly how it computes activation values. Then we take a step back and look at some the important properties of the way in which neural network process information using the Jets and Sharks network as an example.

The Interactive Activation and Competition Mechanism

The activations of each of the units can be thought of as the "degree of belief" in that hypothesis or the existence of that feature. The weights are then an indication of how strongly belief in one hypothesis or feature implies belief in another hypothesis or feature. The Interactive Activation and Competition mechanism, embodied primarily in the activation function, is a cyclic process of updating the belief in a hypothesis according to existing evidence.

Consider a single unit. The evidence on whether it should increase or decrease its activation comes from its incoming weights. If most of the active units in the network (i.e. the hypotheses that the net believes are true) are connected to this unit with positive weights, then we should increase its activation. If most of the active units are connected to this unit with negative weights then its activation should be decreased. The net input function does this by multiplying each of the incoming weights by the level of activation of its unit and adding these values [1]. So the net input for unit i is:

net_i = w_ija_j

where w_ij is the weight from unit j to unit i and a_j is the activation of unit j.

Once the net input has been calculated for all units, activations are updated according to the following equation:

if (net_i < 0)
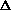a_i = (max - a _i) net_i - decay (a_i - rest)
Otherwise,
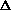a_i = (a _i - min) net_i - decay (a_i - rest)

where 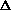a_i is the amount by which we change a_i.

The most important part of this equation is net_i which determines whether the activation of unit i will increase or decrease. If net_i is positive the evidence that this unit should be on is strong and the activation will increase. If it is negative the activation will decrease.

If the activation of a unit is equal to max then the net believes the hypothesis completely. If it is equal to min then the net disbelieves the hypothesis completely. The rest corresponds to an "I don't know state". The (max - a _i) or (a _i - min) terms ensure that the activation remains between min and max and doesn't continue to either grow or shrink without bound [2]. The -decay (a_i - rest) part of the equation forces the activation to return to the rest value in the absence of external input.

Typically, we choose max > 0 >= rest >= min. By default max is set to 1, min is set to -0.2, rest is set to -0.1 and decay is 0.1. To change any of these parameters you first create a global value for that parameter by selecting the appropriate item from the Actions menu. Using the arrow tool you can select that global value and alter its value in the parameter panel at the bottom of the screen. Make sure that you hit return to make the value change.

IAC networks exhibit a number of interesting dynamics including:

Decay: the tendency for a unit to return to the rest value.
Boundaries: the tendency for a unit to remain between the max and min values.
Equilibrium: the point to which a network will settle.
Competition: the tendency for units connected by negative weights to turn each other off. A unit that begins with a small advantage eventually "wins" the competition and becomes active at the expense of the other units in the pool.
Resonance: the tendency for units connected by positive weights to make each other active and keep each other active in the face of external competition.
Blocking and Hysteresis: the ability of one active unit to stop a unit to which it is connected with a negative weight from becoming active.
Oscillation: the ability of some networks turn on and off on consecutive timesteps and never settle to a stable point.

In the next section we will examine these dynamics. Readers wishing to by pass the mathematical detail at this point might like to skip to the section entitled "Back to the Jets and Sharks Network".

The Dynamics of IAC Networks

We can get a feel for the dynamics outlined above by considering a number of special cases:

Decay: Consider what happens when the net input to a unit is zero (i.e. net_i = 0) so that a unit is only subject to the effect of decay. The "otherwise" clause of the if is taken which reduces to -decay (a_i - rest). If the current activation is above rest then a_i is a negative value which moves the activation down. If the current activation is below rest then a_i is positive moving the value up. If a_i = rest then there will be no change, that is, the activation will have settled on the rest value.

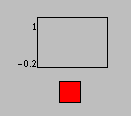
Figure 2: IAC network demonstrating decay.

Exercise 3: To see decay in action and create a IAC network with just one unit (see figure 2, you can select New from the File menu to remove the Jets and Sharks network). Activate the unit. Now create a graph of the value of the unit (by selecting the graph tool and clicking on the unit). Decrease the min value of the graph to -0.2 and run 50 cycles. Describe how the value of the unit decreases and record the level at which it asymptotes.

Boundaries: The activation function is designed to automatically constrain the activation to be between max and min. To see why suppose the decay value is set to zero. Since it has the effect of moving the activation towards rest which lies between min and max ignoring it will not affect the argument. Now, if the net input is positive and a_i is greater than max then a_i = (max - a _i) net_i which will be negative forcing the activation down below max. If the the net input is negative and a_i is less than min then a_i = (a _i - min) net_i which will be positive forcing the activation above min.

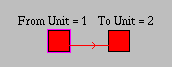
Figure 3: IAC network demonstrating boundaries.

Exercise 4: To see how the boundaries operate, create a network with two units connected by a weight (see figure 3). Now set the weight to 1.0, the from unit to 1.0 and the to unit to 2.0 (outside the boundaries). Freeze the from unit. Run 20 cycles. How long does it take for the activation to move within the boundaries?

Equilibrium: If the net input to an IAC unit is held fixed the unit will eventually settle to an equilibrium point. We can see where this equilibrium point is by setting a_i to zero and solving for a_i. Lets suppose that net_i is positive.

0 = (max - a_i) net_i - decay (a_i - rest)
decay a_i + net_i a_i = max net_i + decay rest
a_i = (max net_i + decay rest) / (decay + net_i)

Assuming max = 1 and rest = 0:

a_i = net_i / (decay + net_i)

a_i = (net_i / decay) / (net_i/decay +1)

The later expression shows how decay acts as a scaling factor on the equilibrium point. Note also that regardless of how large the net input becomes the activation at equilibrium is below one. An equivalent analysis is possible when net_i is negative (see exercise 6).

Exercise 5: Calculate the equilibrium point when net_i = 1, max = 1, rest = -0.1 and decay = 0.1. Now rerun the previous simulation. Does it settle at the appropriate equilibrium point?

Exercise 6: In the text above the equilibrium point is calculated when net_i is fixed and positive. Perform the same calculation for the case where net_i is negative.

So far we have been considering single units with fixed net input. As the name suggests, the Interactive Activation and Competition (IAC) network becomes most interesting when multiple units interact. Different dynamics can be established through the interconnection structure and the values of the weights and in the following sections we will examine some of these.

Competition: Placing units in pools where each unit in the pool is connected to each of the other members by negative weights (with no self weights) sets up a competitive dynamic. Small differences in the net input to units in such a pool become amplified as time progresses. Such a dynamic is useful when the units in the pool represent mutually exclusive hypotheses. For instance, in the Jets and Sharks example a gang member cannot be in their 20s and in their 30s or 40s. Consequently, the units in the "Age" pool are connected by negative weights and as processing continues one of them will eventually win.

To see how competition operates suppose that we have two units connected with weights of -1. Unit 1 receives external input (i.e. input from units other than unit 2) of I₁ and unit 2 receives external input of I₂. Furthermore, lets suppose that decay is zero, the initial activations of the units are zero and max = 1 > I₁ > I₂ > 0 = min.

At the first time step:

a_i = (max - a _i) net_i - decay (a_i - rest)
= (1 - 0) I_i

So a₁ = I₁ and a₂ = I₂

At the second timestep:

net₁ = I₁ - a₂ = I₁ - I₂ and net₂ = I₂ - a₁ = I₂ - I₁

So: 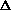a₁ = (1 - I₁)(I₁ - I₂) and 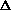a₂ = I₂ (I₂ - I₁)

Because 1 - I₁ and I₂ are positive and I₁ > I₂: 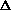a₁ > 0 and 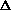a₂ < 0. So a₁ grows while a₂ dies. The stronger a₁ becomes the more it inhibits a₂. The weaker a₂ becomes the less it inhibits a₁.

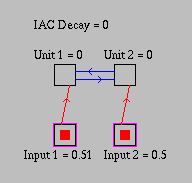
Figure 4: IAC network demonstrating competition between units.

Exercise 7: To see the competitive dynamic in action construct an IAC network with four units (see figure 4). Connect two of the units with weights of -1. These are units 1 and 2. Now connect one of the remaining units to unit one with a positive weight of 1. This unit will provide the external input to unit 1. Set its value to 0.51 and freeze it. Do the same with the remaining unit for unit 2. Set its value to 0.5 and freeze it. Now set the decay value to 0 (by creating a Decay global value - see Actions menu). Do one cycle at a time (for a total of ten cycles) and record how the activations of the two units change.

Resonance: If units are connected by mutually excitatory weights they will tend to make each other active and to keep each other active in the face of decay. This phenomena is called resonance (an analogy to the resonance of waves).

For instance, suppose we have two units connected by excitatory connections with strength 2 x decay. Furthermore, suppose that rest is set to 0 and each unit has an activation of 0.5. How will they change?

a_i = (1 - a _i) net_i - decay a_i
= (1 - 0.5) x 0.5 x 2 x decay - decay 0.5
= 0

So the activations will remain at 0.5 indefinitely, that is, the units will resonate. The above example might leave one with the impression that resonance occurs only when the parameters are carefully selected. This is not the case, although usually the units will not come to have exactly the same values as the next exercise demonstrates.

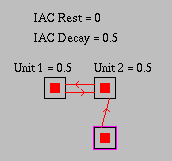
Figure 5: IAC network demonstrating resonance of units.

Exercise 8: To begin with set up the two unit network discussed above. Set decay to 0.5 and the weights to 1. Set rest to 0 and the activations of the units to 0.5. Now cycle. The units should retain their initial activations. Now add a third unit and connect it with a weight of 1 (see figure 5). Set its activation to 0.5 and freeze it. Now cycle for 40 timesteps. What happens to the activations of the two units?

Blocking and Hysteresis: The initial state of a network can have long term consequences for the way that the units respond to external input. A unit which is initially active can slow down the response of another unit (hysteresis) or in extreme cases block it completely.

Suppose we have two units with mutually inhibitory connections of -2 decay. Unit 1 begins with an activation of 0.5 and both units have external input of decay. Supposing rest is 0:

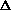a₁ = (1 - a ₁) net₁ - decay a₁
= (1 - 0.5) decay - decay x 0.5
= 0

a₂ = (a ₁ - min) net₂ - decay a₂
= (a ₂ - min) (-2 decay x 0.5 + decay) - decay x 0
= 0

The activation of unit 1 will be maintained at 0.5, but despite a positive external input the activation of unit 2 will remain at zero. Unit 2 is being blocked by the activation of the unit 1.

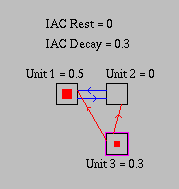
Figure 6: IAC network demonstrating blocking.

Exercise 9: Construct the network outlined above with rest set to zero, and decay set to 0.3 - so the negative weights are set to -0.6 (see figure 6). Freeze unit 3 at 0.3 and connect it with weights of 1 to both unit 1 and 2. Cycle to demonstrate that unit 2 is blocked by unit 1. Now delete the weight from unit 3 to unit 1 and cycle. What happens to the activation of unit 2?

Oscillation: Up to this point we have concentrated on networks which settle to a steady state of activation. While this is often the case, IAC networks can oscillate (i.e. enter a limit cycle) given the appropriate parameters. Figure 7 shows such a network and Exercise 10 outlines how to construct it.

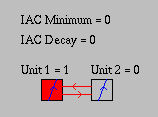
Figure 7: IAC network demonstrating oscillation.

Exercise 10: Create two units. Connect them with positive weights set to 1. Create self weights set to -1 (see figure 7). Set the decay to 0 and the minimum to 0. Now toggle one of the units so that its activation is 1 and run 20 cycles. Describe the behaviour of the units.
Exercise 11: Calculate 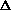a₁ and 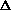a₂ and explain how the network oscillates.

Back to the Jets and Sharks Network

Now that you have a more in depth understanding of how the IAC network operates lets return to the exercises performed in the introductory section. Reset the Jets and Sharks network and activate the Art instance unit using the toggle tool. Click on the cycle button.

Exercise 12: Why is Ralph's instance unit active?

Exercise 13: Why isn't the Ralph name unit active?

Exercise 14: Cycle for another 90 cycles (making a total of 100 cycles). What happens to Ralph's name unit? Why?

Exercise 15: Why are some of Art's features more active than others? Note: you can select the arrow tool and click on a unit to see its exact activation in the parameter panel at the bottom of the screen.

Now click on the reset button to return all of the units to zero activation and activate the instance unit for Art and the pusher and bookie units. Now run one cycle.

Exercise 16: What are the activations of the bookie, pusher and burglar units after one cycle?

Exercise 17: Why is the pusher unit more active than the bookie unit?

Exercise 18: Explain the activation of the burglar unit.

How Neural Networks Process Information

Neural networks process information in a very different way from standard computers based on the Von Neumann architecture. Whereas Von Neumann machines rely on discrete sequential processing, neural networks are highly parallel and continuous in nature. These differences are important both in terms of designing useful devices and because they seem to provide a closer match to the way that people operate. There are four properties of neural networks that we will be demonstrating. These are:

Content addressability - the ability to access memories given any of the components of the fact or episode.
Robustness to noise - the ability to access memories despite incomplete or even incorrect cues.
Generalization - the ability to generalise over a set of instances.
Default assignment - the ability to assign plausible default values if a given fact is not in memory.

Content Addressability

In a Von Neumann architecture data is stored at specific locations or addresses in the computer's memory. In order to retrieve that data it's unique address must be known. Similarly, in relational databases information is stored in rows of a table and certain fields of each row are designated as the "keys" for that record. The data in these fields is usually unique and the database is optimised for queries that use these fields to retrieve the row.

Contrast this with human memory. We can be reminded of facts and episodes from what are often quite obscure cues which are often not unique when taken in isolation. We are able to locate records (or memories) based on any of the information stored in that record. For instance, if I say to a friend, "I like your blue shirt with the stripes.", they will often know exactly which one I'm talking about, despite the fact that I have not provided a unique identifier for that shirt. Furthermore, the cues given, that is, blue and striped, may only specify the shirt uniquely when taken in combination (if your friend has other blue shirts and other striped shirts).

Of course, it is possible with the appropriate query to retrieve the same information from a computer database. In human memory, however, retrieval from the content of a memory is automatic - human memory is fundamentally content addressable.

Exercise 19: To illustrate content addressability in the Jets and Sharks network, first reset the activations. Now activate the Jet, and 30's units and run 10 cycles. These characteristics while not unique individually do specify a unique gang member when taken together. Who is it?

Robustness to Noise

Von Neumann architectures are discrete in nature. This discrete nature allows them to retain information completely faithfully when subjected to small amounts of noise. Provided the noise is not sufficient to switch a bit from a one to a zero or vice versa the information will be interpreted as intended. This is, of course, the secret behind the improved performance of digital recording. For a great many applications this is a very useful property. I would prefer that the bank retained the exact balance of my account, not an approximation or best guess.

In contrast, neural networks use redundancy in their structure to provide a best guess of the information to be retrieved. Such an approach is very useful in situations of extreme noise (such as speech recognition) where the information is incomplete or even incorrect. The next exercise demonstrates how the IAC network is resistant to erroneous information.

Exercise 20: Reset the Jets and Sharks network and toggle the Shark, 30's, H.S., Burglar and Married units. These are the characteristics of Rick except that Rick is actually Divorced not Married (see table 1). Now run 10 cycles. Which name unit comes on?

Exercise 21: The Lance unit also becomes partially active. Why?

Exercise 22: Why does the Lance instance unit deactivate?

Exercise 23: Run another 40 cycles. What happens to the marital status units?

Generalization

One operation that people seem to be very good at is collapsing over a set of instances to establish a general trend. For instance, we might ask "Are Americans more extroverted than Australians?". Unless you have read the studies claiming that in fact they are, then your only recourse would be to collapse across the set of Americans and the set Australians you know and to extract some form of central tendency measure on the extrovert/introvert dimension. This is quite a difficult computation, but one that people perform routinely. The IAC network can accomplish spontaneous generalisation of this kind by activating a property and cycling.

Exercise 24: To ask the question "What are Single gang members like?" reset the network and toggle the Single unit on. Run ten cycles. Which characteristics become active?

Exercise 25: The Art and Ralph instance units become active but not the Sam instance unit, despite the fact that Sam is Single also. Why is this?

Exercise 26: Why does the 40s unit become active?

Default Assignment

The final property that we will examine is the ability of the IAC network to provide plausible default values if it does not "know" a given piece of information. The human memory system makes extensive use of plausible defaults. In fact, people can have difficulty distinguishing actual memories from those that have been reconstructed from other related information. In the IAC network the provision of plausible defaults is closely related to generalisation. Items which are similar to the target item are used to extrapolate what the missing information should be. In the following exercise we will remove some of the weights in the Jets and Sharks network and see if it can provide reasonable answers.

Exercise 27: Firstly, reset the network, toggle the Ralph instance unit on and run 10 cycles. Note which properties become active. Now use the delete tool to remove the weights between the Ralph instance unit and the 30s unit and the Ralph instance unit and the Single unit (remove the weights both to and from the units - that is 4 weights all up). Reset the network, toggle the Ralph instance unit on and run 30 cycles. How successful was the network at guessing Ralph's age and marital status properties? Explain the results.

Here endth the IAC tutorial. If you are interested in the IAC mechanism see the Word Superiority network (in the Networks menu) which uses the same mechanism to model people's ability to recognise letters in the context of words.

References

McClelland, J. L. (1981). Retrieving general and specific information from stored knowledge of specifics. Proceedings of the Third Annual Meeting of the Cognitive Science Society, 170-172.

McClelland, J. L., & Rumelhart, D. E. (1981). An interactive activation model of context effects in letter perception: Part 1. An account of basic findings. Psychological Review, 88, 375-407.

McClelland, J. L. & Rumelhart, D. E. (Eds.). (1988). Explorations in parallel distributed processing: A handbook of models, programs, and exercises. Cambridge, MA: MIT Press.

Rumelhart, D. E., & McClelland, J. L. (1982). An interactive activation model of context effects in letter perception: Part 2. The contextual enhancement effect and some tests and extensions of the model. Psychological Review, 89, 60-94.

Rumelhart, D. E., & McClelland, J. L. (Eds.). (1986). Parallel distributed processing: Explorations in the microstructure of cognition (Vol. 1). Cambridge, MA: MIT Press.

Endnotes

[1] In the McClelland and Rumelhart formulation, negative activations coming from other units are set to zero before entering into the net input calculation. For simplicity's sake we have not included this thresholding process. This restriction has little impact on the major points we are trying to address.

[2] In the McClelland and Rumelhart version an activation which falls outside of the boundaries it is set either to max or min which ever is closest. This prevents the activations from becoming very large or very small quickly which can occur if parameter values are large. We have not included this component so that the natural tendency of the activation to keep activations within bounds can be observed. Be warned, though. If your activations are growing very large you may need to decrease some of the parameter values.

The BrainWave homepage.