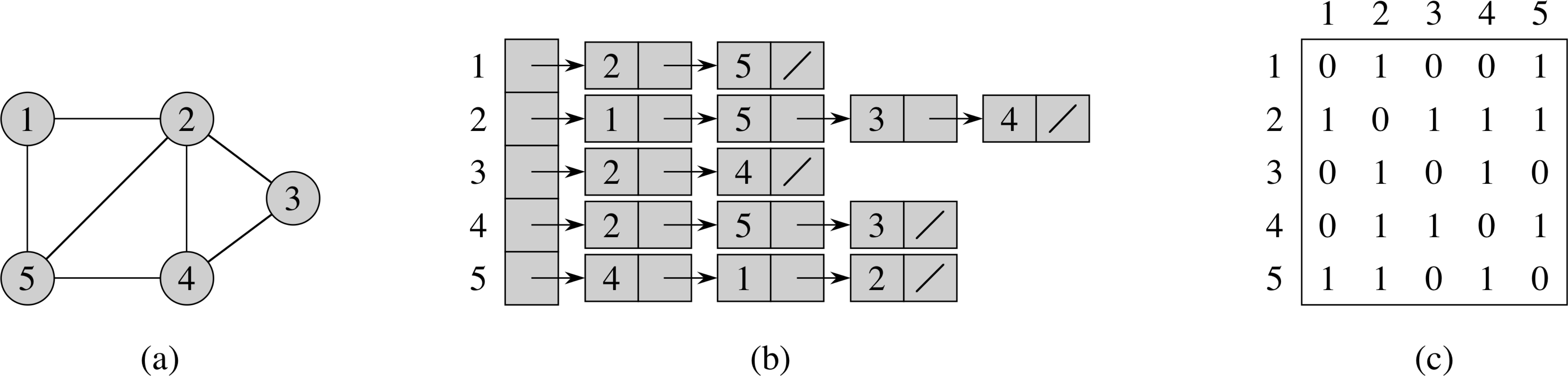
Representing Graphs: Undirected

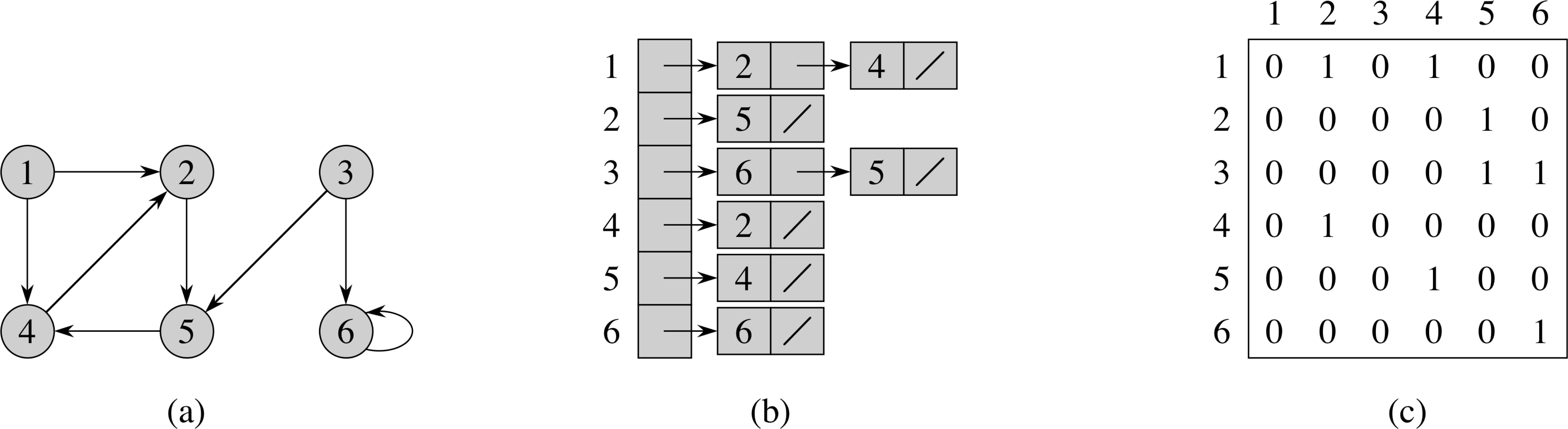
Representing Graphs: Directed

Finding Universal Sink

  Is-Sink(A, k)
  1   let A be |V|×|V|
  2   for j = 1 to |V|
  3      if akj == 1
  4         return FALSE
  5   for i = 1 to |V|
  6      if aik == 1 and i ≠ k
  7         return FALSE
  8   return TRUE
		

  Universal-Sink(A)
  1   let A be |V|×|V|
  2   i = j = 1
  3   while i≤|V| and j≤|V|
  4      if aij == 1
  5          i = i + 1
  6      else
              j = j + 1
  7   if i > |V|
  8      return “no universal sink”
  9   elsif Is-Sink(A,i) == FALSE
 10      return “no universal sink”
 11  else
           return i “is a universal sink”
		

Quick Recap

• Breadth First Search
  • Start at a node s
  • O(|V|+|E|) time
  • Use a queue to maintain unvisited vertices
  • Annotate each node u with u.d, which represents the shortest path from s to u
  • Build a predecessor sub-graph (It is actually a tree. Why?)
• Depth First Search
  • May repeat at multiple vertices (unlike BFS)
  • Annotate each vertex, u, with discovered (u.d) and finished (u.f) times; u.d < u.f
  • Predecessor graph is a depth-first forest

Properties of DFS

DFS: Example

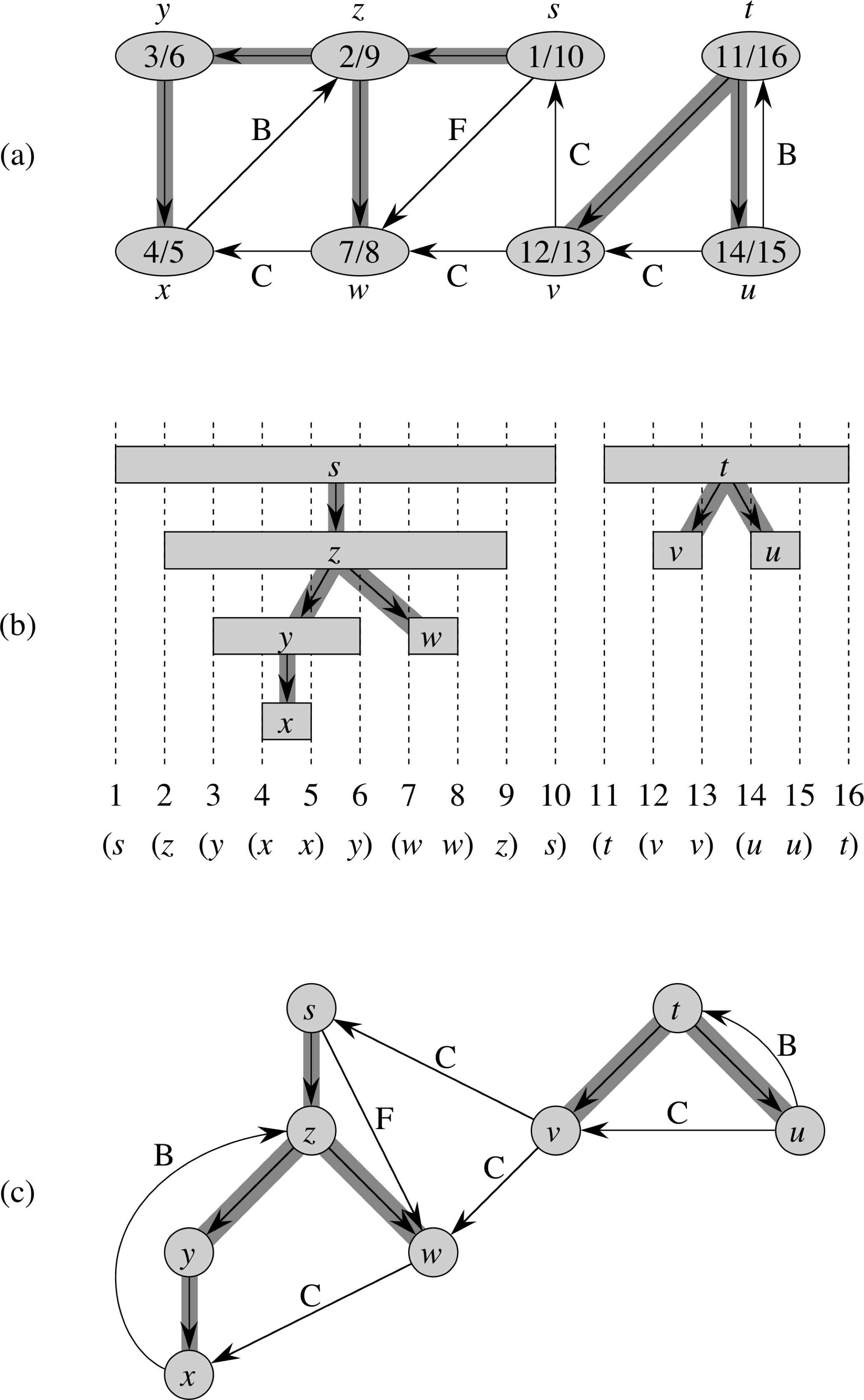
DFS: Four Types of Edges

• Tree edges: Part of the depth-first forest
• Back edges: (u.v) connecting u to an ancestor, v, of u
• Forward edges: Non-tree edge (u,v) connecting u to a descendant, b, of u
• Cross edges: All other edges

Theorem In depth-first search of an undirected graph every edge is either a tree edge or a back edge.

Claim An undirected graph is cyclic if an only if there exist back edges after a depth-first search of the graph.

Topological Sort

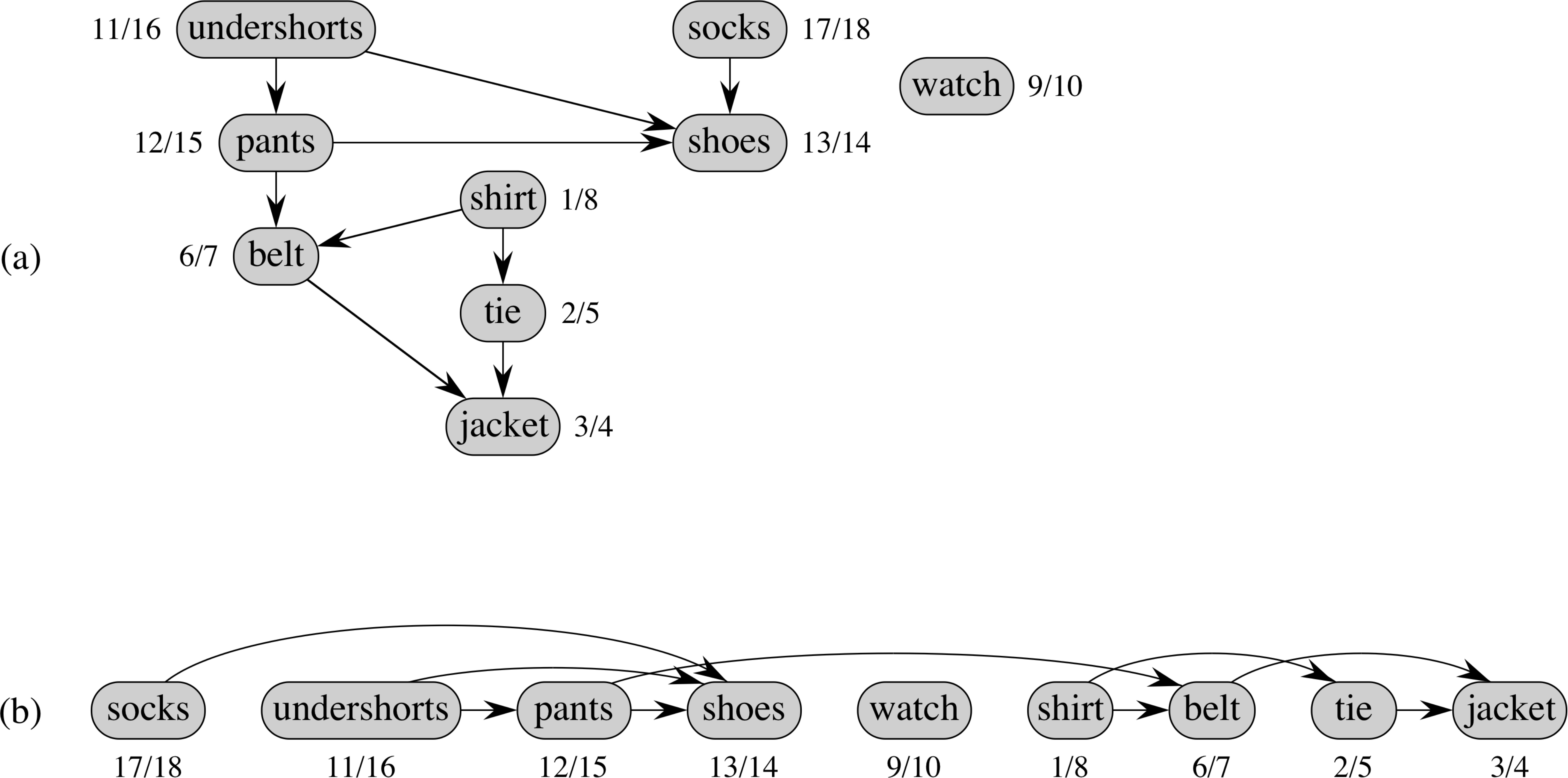
  Topological-Sort(G)
  1   call DFS(G) to compute finishing times v.f for each vertex v
  2   as each vertex is finished, insert it onto the front of a linked list
  3   return the linked list of vertices
	

Why does this work?

Questions

• Give a linear-time algorithm to find the number of simple paths from vertex s to vertex t in a DAG.
• Give an algorithm that determines whether or not a give undirected graph G = (V,E) contains cycle in O(|V|) time.
• Suppose we attempt to topologically sort a graph by repeatedly removing a vertex with in-degree 0 and all its outgoing edges. Why does this work? What happens if the graph has cycles?

Strongly Connected Components

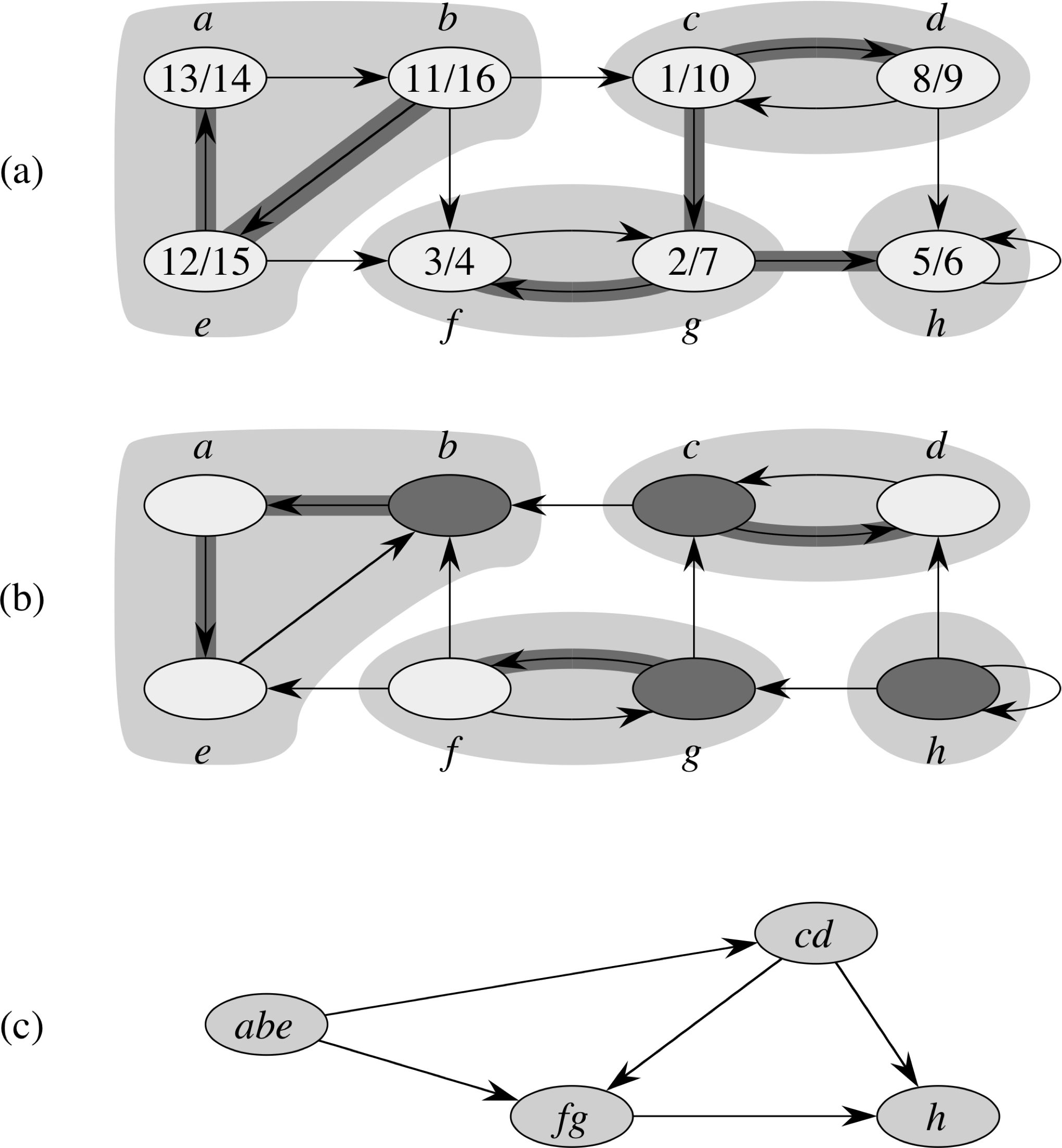
Strongly Connected Components

  Strongly-Connected-Components(G)
  1   call DFS(G) to compute finishing times u.f for each vertex u
  2   compute GT
  3   call DFS(GT), but in the main loop of DFS, consider the vertices in
  order of decreasing u.f
  4   output the vertices of each tree in the depth-first forest formed in line 3 as a separate strongly connected component
	

Why Does the Algorithm Work?

Lemma Let C and C' be distinct strongly connected components in directed graph G = (V,E), let u, v ∈ G, let u', v' &isin C', and suppose that G contains a path u→u'. Then G cannot also contain a path v'→v.

Definition If U ⊆ V, then d(U) = min_u∈U {u.d}, and f(U) = max_u∈U {u.f}

Lemma Let C and C' be distinct strongly connected components in directed graph G = (V,E). Suppose that there is an edge (u,v) ∈ E, where u ∈ C and v ∈ C'. Then f(C) > f(C').

Corollary Let C and C' be distinct strongly connected components in directed graph G = (V,E). Suppose that there is an edge (u,v) ∈ E^T, where u ∈ C and v ∈ C'. Then f(C) < f(C').

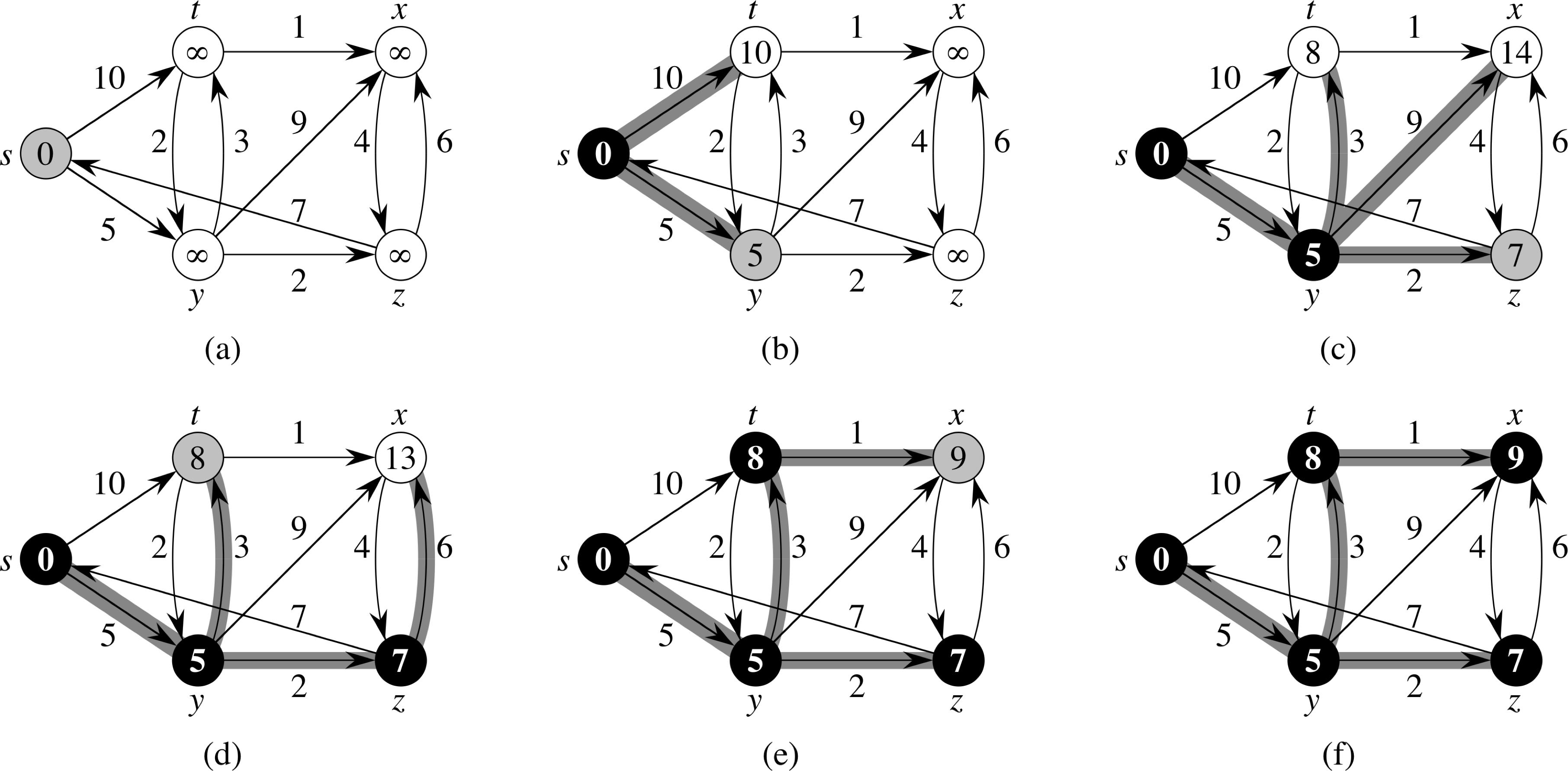
Single-Source Shortest Paths

Given a weighted, directed graph G = (V,E), with weight function w: E → ℜ. The weight w(p) of path p = ⟨v₀, v₁, ..., v_k⟩ is the sum of the weights of its constituent edges:

w(p) = Σki=1 w(v_i−1,v_i)

Define the shortest-path weight δ(u,v) from u to v by:

A shortest path from vertex u to vertex v is any path p with weight w(p) = δ(u,v)

Subpaths are Shortest Paths

Lemma Given a weighted, directed graph G = (V,E) with weight function w: E → ℜ, let p = ⟨v₀, v₁, ..., v_k⟩ be a shortest path from vertex v₀ to v_k and, for any i and j such that 0 ≤ i ≤ j ≤ k, let p_ij = ⟨v_i, v_i+1, ..., v_j⟩ be the subpath of p from vertex v_i to v_j. Then p_ij is a shortest path from v_i to v_j.

Proof By cut-and-paste argument, as before.

Observations

• Negative weight edges are fine
• Negative weight cycles cause the problem to be ill-defined. Why?
• Shortest paths can be represented using the predecessor sub-graph (as DFS-forests and BFS-trees)

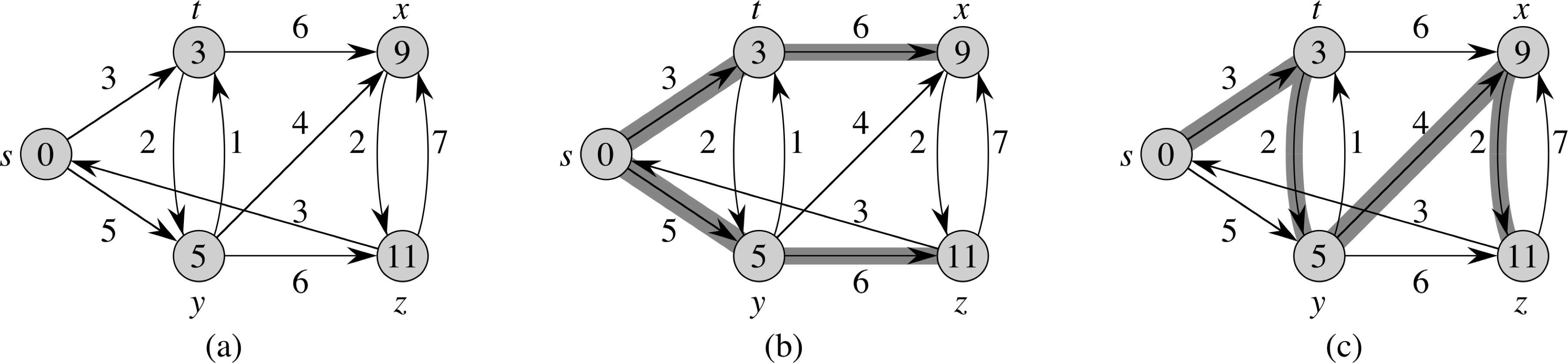
Two Key Steps

  Initialize-Single-Source(G, s)
  1   for each vertex v ∈ G.V
  2      v.d = ∞
  3      v.π = NIL
  4   s.d = 0
		

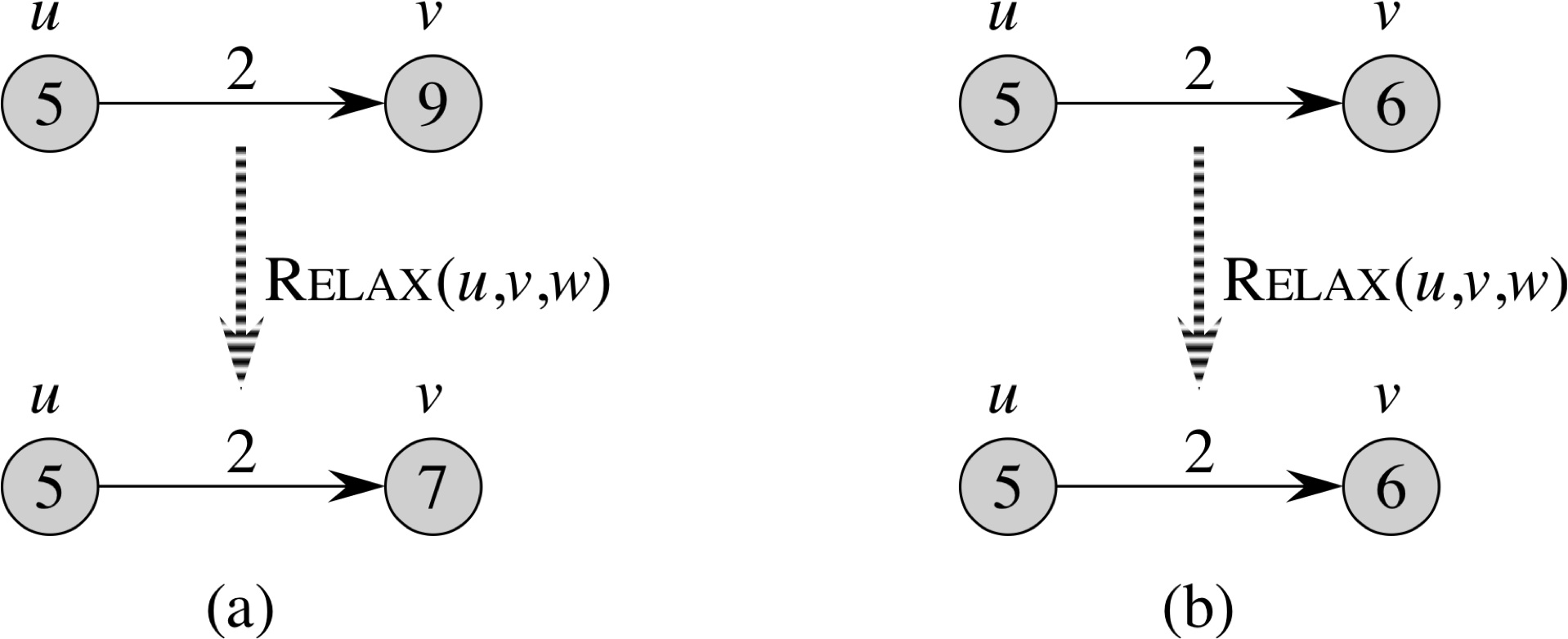
  Relax(u, v, w)
  1   if v.d > u.d + w(u.v)
  2      v.d = u.d + w(u,v)
  3      v.π = u
		

Bellman-Ford Algorithm

  Bellman-Ford(G, w, s)
  1   Initialize-Single-Source(G, s)
  2   for i = 1 to |G.V|-1
  3      for each edge (u,v) ∈ G.E
  4         Relax(u, v, w)
  5   for each edge (u,v) ∈ G.E
  6      if v.d > u.d + w(u,v)
  7         return FALSE
  8   return TRUE
	

Running Time = O(VE)

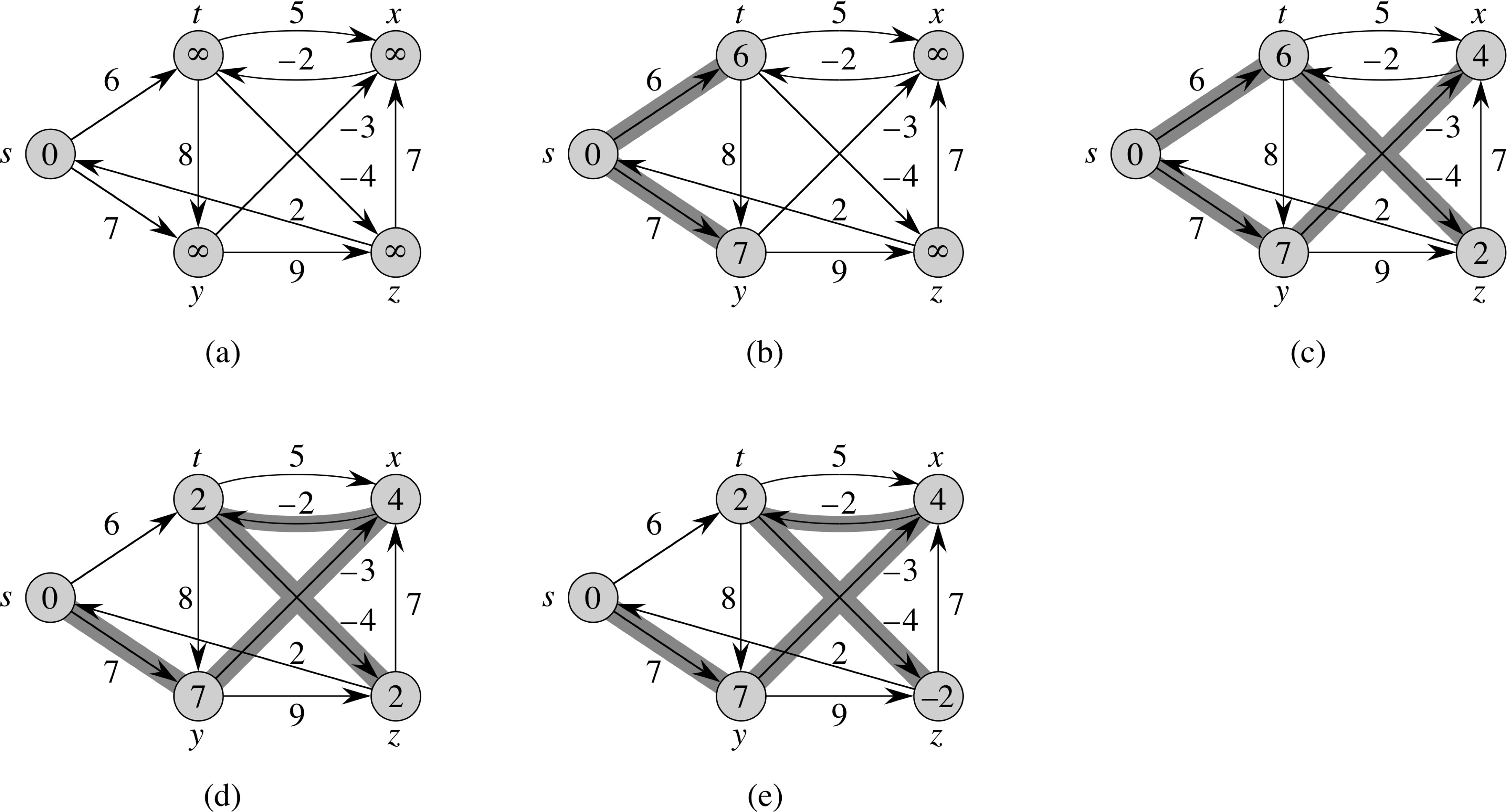
Shortest Path for DAGs

  DAG-Shortest-Paths(G, w, s)
  1   topologically sort the vertices of G
  2   Initialize-Single-Source(G, s)
  3   for each vertex u, taken in topologically sorted order
  4      for each vertex v ∈ G.Adj[u]
  4         Relax(u, v, w)
	

Running Time = Θ(V + E)

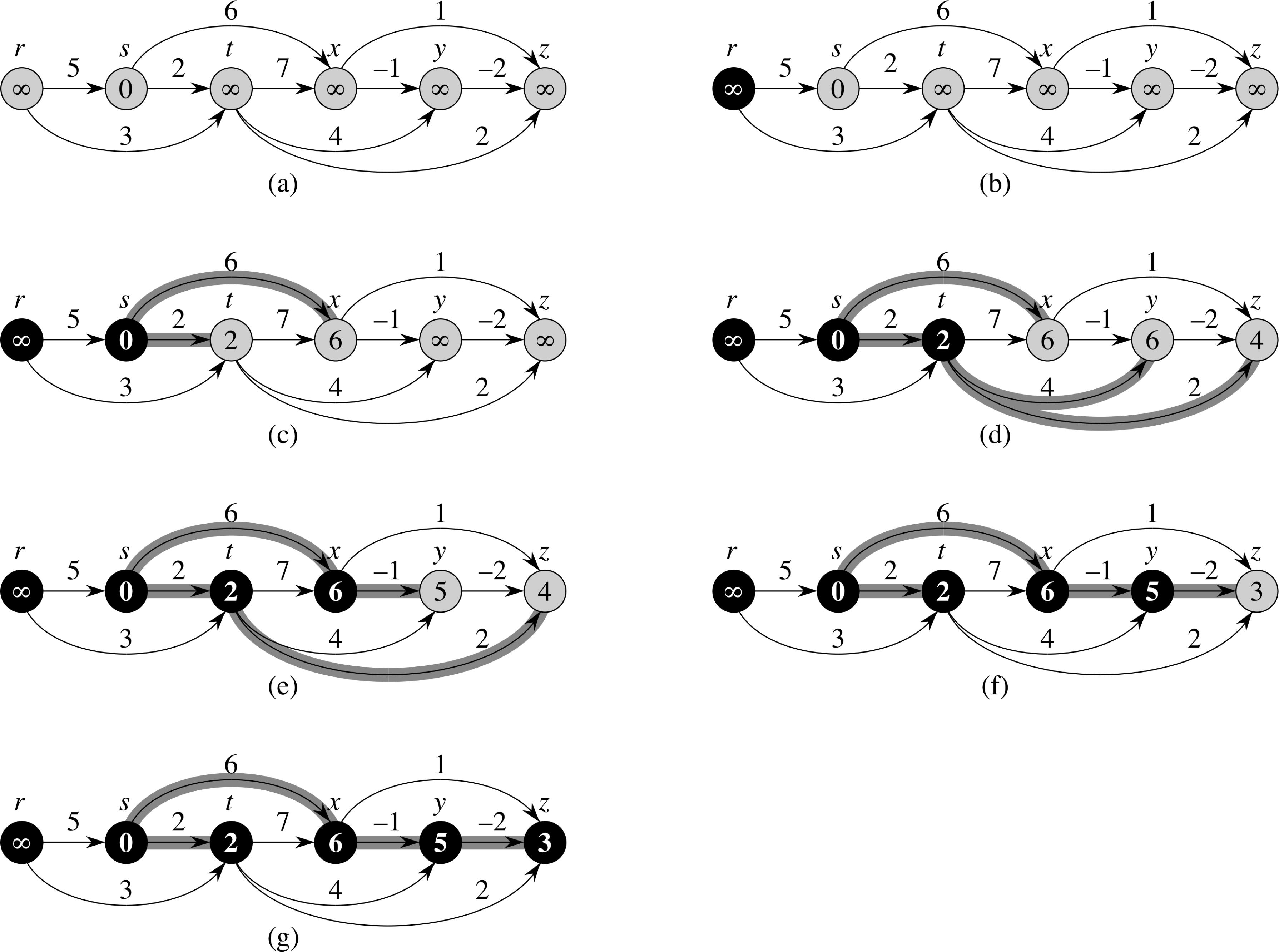
Dijkstra's Algorithm

  Dijkstra(G, w, s)
  1   Initialize-Single-Source(G, s)
  2   S = φ
  3   Q = G.V
  4   while Q ≠ φ
  5      u = Extract-Min(Q)
  6      S = S ∪ {u}
  7      for each vertex v ∈ G.Adj[u]
  8         Relax(u, v, w)
	

Running Time = O((V + E)⋅log(V)) (O(V⋅log(V) + E) achievable)