All animals and automata exhibit some kind of behavior; they do something in response to the inputs that they receive from the environment they exist in. Some animals and automata change the way they behave over time; given the same input, they may respond differently later on than they did earlier on. Such agents learn. The field of machine learning studies learning algorithms, which specify how the changes in the learner's behavior depend on the inputs received and on feedback from the environment.
Learning algorithms fall into three groups with respect to the sort of feedback that the learner has access to. On the one extreme is supervised learning: for every input, the learner is provided with a target; that is, the environment tells the learner what its response should be. The learner then compares its actual response to the target and adjusts its internal memory in such a way that it is more likely to produce the appropriate response the next time it receives the same input. We can think of learning a simple categorization task as supervised learning. For example, if you're learning to recognize the sounds of different musical instruments, and you're told each time what the instrument is, you can compare your own response to the correct one.
On the other extreme is unsupervised learning: the learner receives no feedback from the world at all. Instead the learner's task is to re-represent the inputs in a more efficient way, as clusters or categories or using a reduced set of dimensions. Unsupervised learning is based on the similarities and differences among the input patterns. It does not result directly in differences in overt behavior because its "outputs" are really internal representations. But these representations can then be used by other parts of the system in a way that affects behavior. Unsupervised learning plays a role in perceptual systems. Visual input, for example, is initially too complex for the nervous system to deal with it directly, and one option is for the nervous system to first reduce the number of dimensions by extracting regularities such as tendencies for regions to be of constant color and for edges to be continuous.
A third alternative, much closer to supervised than unsupervised learning, is reinforcement learning: the learner receives feedback (sometimes) about the appropriateness of its response. For correct responses, reinforcement learning resembles supervised learning: in both cases, the learner receives information that what it did is appropriate. However, the two forms of learning differ significantly for errors, situations in which the learner's behavior is in some way inappropriate. In these situations, supervised learning lets the learner know exactly what it should have done, whereas reinforcement learning only says that the behavior was inappropriate and (usually) how inappropriate it was. In nature, reinforcement learning is much more common than supervised learning. It is rare that a teacher is available who can say what should have been done when a mistake is made, and even when such a teacher is available, it is rare that the learner can interpret the teacher's feedback to provide direct information about what needs to be changed in the learner, that is, features of the learner's nervous system. Consider an animal that has to learn some aspects of how to walk. It tries out various movements. Some work — it moves forward — and it is rewarded. Others fail — it stumbles or falls down — and it is punished with pain.
Thus while much of the focus of machine learning has been on supervised learning, if we are to understand learning in nature, we need to study unsupervised and reinforcement learning. With the SMARTS program, you will explore one reinforcement learning algorithm in some detail. You will also see how we can implement reinforcement learning using a familiar supervised learning algorithm.
(For more on reinforcement learning, see this tutorial by M. E. Harmon and S. S. Harmon)
To simulate the learning of real biological systems, we need to make some simplifying assumptions about our agent and its behavior. (From now on, I'll refer to our learner as an "agent" to emphasize that it's actively doing things, not just learning what to do.) We will assume that the agent's life is a Markov decision process. That is,
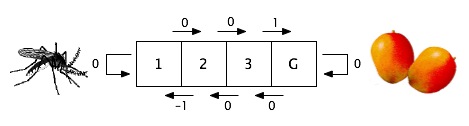
For example, consider an agent in a one-dimensional world of cells. In each cell except those on the end, the agent can go either east or west. At the extreme west end lives a swarm of mosquitoes. At the extreme east, there is a mango tree. Anywhere else, the agent receives no information at all from the environment. The agent can sense which cell it is in, but at the beginning of learning, it has no idea what cell it gets to by going east or west and what sort of reinforcement it will receive, if any. On the basis of the punishment it receives if and when it reaches the west end and the reward it receives if and when it reaches the east end, it must learn how to behave anywhere in the world.

The goal of reinforcement learning is to figure out how to choose actions in response to states so that reinforcement is maximized. That is, the agent is learning a policy, a mapping from states to actions. We will divide the agent's policy into two components, (1) how good the agent thinks an action is for a given state and (2) how the agent uses this knowledge to choose an action for a given state.
There are several ways to implement the learning process. We will focus on just one, Q learning, a form of reinforcement learning in which the agent learns to assign values to state-action pairs, that is, the first component of the agent's policy. We need first to make a distinction between what is true of the world and what the agent thinks is true of the world. First let's consider what's true of the world. If an agent is in a particular state and takes a particular action, we are interested in any immediate reinforcement that's received because it's relevant for the agent's policy. But we (and the agent) are also interested in any future reinforcements that result from ending up in a new state where further actions can be taken, actions that follow a particular policy. For example, in the mosquito-mango world above if the agent is in cell 2, moving to the east results in no reinforcement, but it puts the agent in the position to get a positive reinforcement on the next action (given the right policy). Given a particular action in a particular state followed by behavior that follows a particular policy, the agent will receive a particular set of reinforcements. This is a fact about the world. In the simplest case, the Q-value for a state-action pair is the sum of all of these reinforcements, and the Q-value function is the function that maps from state-action pairs to values. But the sum of all future reinforcements may be infinite when there is no terminal state, and besides, we may want to weight the future less than the here-and-now, so instead a discounted cumulative reinforcement is normally used: future reinforcements are weighted by a value γ between 0 and 1 (see below for mathematical details). A higher value of γ means that the future matters more for the Q-value of a given action in a given state.
If the agent knew the Q-values of every state-action pair, it could use this information to select an action for each state. The problem is that the agent initially has no idea what the Q-values of any state-action pairs are. The agent's goal, then, is to settle on an optimal Q-value function, one that assigns the appropriate values for all state/action pairs. But Q-values depend on future reinforcements, as well as current ones. How can the agent learn Q-values when it only has access to immediate reinforcement? It learns using these two principles, which are the essence of reinforcement learning:
The second principle is the one that makes the reinforcement learning magic happen. It permits the agent to learn high or low values for particular actions from a particular state, even when there is no immediate reinforcement associated with those actions. For example, in our mosquito-mango world, the agent receives a reward when it reaches the east end from the cell just to the west of it. It now knows that that cell is a good one to go to because you can get rewarded in only one move from it.
What's left is the mathematical details. First, consider the optimal Q-value function, the one that represents what's true of the world.
That is, the optimal Q-value for a particular action (at) in a particular state (st) is the sum of the reinforcement received when that action is taken and (the blue part of the equation) the discounted best Q-value for the state that is reached by taking that action (st+1). The agent would like to approach this optimal value for each state-action pair. At any given time during learning, the agent stores a particular Q-value for each state-action pair. At the beginning of learning, this value is random or set at some default. Learning should move it closer to its optimal value. In order to do this, the agent repeatedly takes actions in particular states and notes the reinforcements that it receives. It then updates the stored Q-value for that state-action pair using the reinforcement received and the stored Q-values for the next state. Assuming the Q-values are stored in a lookup table, the agent could use this update equation, the Q learning rule:
This sets the Q-value to be the sum of the reinforcement just received and the discounted best Q-value for the next state, that is, what the agent currently believes the Q-value for the next state to be (what is stored in its lookup table). But this is usually a bad idea because the information just received may be faulty for one reason or another. It is better to update more gradually, to use the new information to move in a particular direction, but not to make too strong a commitment. Before we discuss a solution to this problem, let's consider how the information about Q values should actually be represented within the "brain" of the agent.
So far what we have been considering is a "brain" that stores a Q value for every state-action combination in a lookup table, that is, a matrix with a row for every state and a column for every action. This approach makes sense where there are small number of such combinations. But when the number gets very large, it becomes impractical because a cell in the table for a state s and an action a will remain empty until the agent gets information about that combination, and this can only happen if it actually tries the action in that state. The possibility of doing this obviously decreases as the number of states and actions increases. The problem is that, with no information about one or more of the actions in a given state, the agent will not know how to behave when in that state.
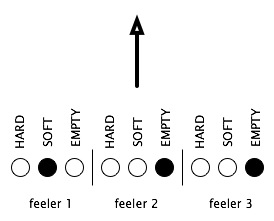
Instead of a lookup table, we can implement the Q value memory in the form of a simple neural network. In place a single row in the table for a given state, we represent each state as a distributed pattern of activation over a set of neural network units in the input layer of a network. Each unit represents a state feature rather than a state. If each agent had three feelers that could sense three different texture in one are of its surroundings, the input layer of the neural network might look like this. Each of the circles is a unit; a white unit is "off" (inhibited), and a black unit is "on" (activated).
Now we can represent each of the agent's actions with a single output unit. So if the agent has three options, moving, turning, and resting, the neural network would look like this. Each of the arrows connecting an input to an output unit represents a single weight in the network. The weights out of the "bias" unit, which is always activated, represent the bias for each output unit, that is, its general tendency to be activated or inhibited.
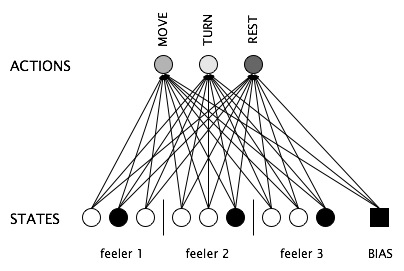
This neural network replaces the Q value lookup table. To look up the Q value for a given state, we present the pattern of activation representing the state in terms of its features. Then we pass this activation to the output units through the weights. Each output unit receives an amount equal to the dot product of the weights into it and the input pattern, that is, the sum of the pairwise products of input unit activations and corresponding weights.
Now how do we train such a network using the Q learning rule? We can use a neural network learning algorithm like the delta rule or back-propagation, but only if we have a target for each input pattern. This is because these algorithms are a supervised. But the Q learning rule gives us a target. That is, for each input pattern the agent is presented and consequent action taken, the agent receives two pieces of information that give it an estimate of what the Q value for that state-action pair should be: the immediate reinforcement received and the next state, for which the agent has its own estimate of the best Q value. These two pieces of information correspond to the two terms in the Q learning rule, repeated here for convenience. Now the s's representing the states are in bold to emphasize that they are vectors, that is, patterns, rather than scalar values.
The first term, the reinforcement, is a simple matter because the agent receives it directly from the world. The second term, shown in blue above, the estimated best Q value of the next state, requires one more step. The next state in the neural-network version of the algorithm is a pattern, not a single value. In order to estimate the best Q value for this state, the agent feeds this pattern into its neural network, reads off the values of the output units and picks the highest one. Note that this value represents what the agent currently believes to be the best Q value for the next state; how close this is to the actual value should grow with experience.
Training a neural network with multiple output units normally requires a target for each, but in our case, we have only one value: the number returned by the Q learning rule. This number applies to only one action, the action that the agent took and that led to the reinforcement and the next state. Recall that this action is represented by a single output unit. For example, if the action selected by the agent is a turn, then for the neural network in the figure above, there is a target for the second unit, but not the others. But this is not a problem if we realize that we only want to update the weights into the unit representing the action selected. We just treat the other output units as though their values are correct since we have no information about them.
It is beyond the scope of this page to go into the details of supervised learning algorithms, so we'll just summarize here how the delta rule works. This rule is appropriate for a neural network with no hidden units, that is, no units between the input and the output. It is an example of a gradient descent learning algorithm; on each presentation of an input pattern and a target, it gets information about what direction to move each weight in, and the weights are adjusted in that direction by a small amount. We can simplify the usual learning rule in one way because we do not "squash" the output unit activations to a value between 0 and 1 (or -1 and 1) as is usually done. This is because we want to the output unit activations to represent Q values, and these are not constrained to fall between in some special range. So for our output units, their activation is whatever input they get from the input pattern. With this simplification, here is the equation for the change in the weight that connects input unit i to output unit j.
In the equation, tj is the target for the jth output unit; xi and xj are the activations of the ith input unit and the jth output unit (after the output units have been activated); and η is the learning rate, a number between 0 and 1 that governs how fast learning takes place. Given a learning rate less than 1, we now have the answer to the problem of adjusting the Q values too quickly; on the basis of one training trial (state, action, reinforcement, next state), we just use the new information to adjust the Q value (that is, the weights) but only to move some distance in the direction specified by the information.
Combining the learning rule with the expression for the target above (shown in red), we get the following for the change in a weight at time t into the output unit for the action selected. Here j(at) is the index among the output units for the selected action, at; si is the activation of the ith state (input) unit; Q(s, j) is the activation of the jth output when the state pattern s has been presented to the network; and Q(s) is the vector of activations of all of the output units when state pattern s has been presented.
There is no change in the weights into the other output units.
An important aspect of reinforcement learning is the constraint that only Q-values for actions that are actually attempted in states that actually occurred are updated. Nothing is learned about an action that is not tried. The upshot of this is that the agent should try a range of actions, especially early on in learning, in order to have an idea what works and what doesn't. More precisely, on any given time step, the agent has a choice: it can pick the action with the highest Q-value for the state it is in (exploitation), or it can pick an action randomly (exploration). Note that there is a tradeoff between these two strategies. Exploitation, because it is based on what the agent knows about the world, is more likely to result in benefits to the agent. On the other hand, exploration is necessary so that actions that would not be tried otherwise can be learned about. We formalize the action decision process in terms of probabilities. The simplest possibility is to flip a coin and with a certain probability exploit your knowledge (pick the action with the highest Q-value) or explore (pick a random action). It also makes sense to have the probability of exploration depend on the length of the time the agent has been learning. Early in learning, it is better to explore because the knowledge the agent has gained so far is not very reliable and because a number of options may still need to be tried. Later in learning, exploitation makes more sense because, with experience, the agent can be more confident about what it knows.
The action selected should also depend on its Q value relative to the others for the given state; when the highest Q value is much higher than the others, it should have a greater probability of being selected than when the highest Q value is only slighter higher than the other values. Because these are still probabilities, there is still a chance of picking an action that currently has a low Q-value; that is, exploration is possible throughout learning and is more likely the nearer the Q-values for the current state are to one another. Here is one way of accomplishing this:
where the as represent all of the possible actions in state st, n is the number of decisions that have been made (that is, the "age" of the agent), and E is a constant between 0 and 1 that determines how how much the probability depends on age and relative Q values. Keeping all of the other values constant, this equation means that the probability of selecting an action becomes greater (1) as the Q value for that action in the current state increases relative to the Q values for the other actions, (2) as age increases, and (3) as E increases.
The task of the critters in the learning version of SMARTS is essentially the same as that in the evolution version: to figure out how to behave in different circumstances. Q learning is based on the notions of states and actions. An agent's states are what its sensors detect of the world around it. In the SMARTS program, critters have only simple touch sensors which can tell the texture of one or more of the cells that immediately surround the critter. In the learning version of the program, there are only four possibilities for the contents of a cell: either it is empty or it contains a plant, a rock, or another critter. All four of these "textures" are distinguishable by the critter's sensors, and these represent the possible states that are relevant for Q learning. As is usual at the start of Q learning, the critters initially know nothing about what the different states mean, that is, which actions are appropriate in the context of which states.
In the learning version of the program, critters have seven possible actions: they can attempt to move forward one cell, turn in one of the five possible directions, or do nothing (rest). What happens when a move is attempted depends on what's in the cell in front of the critter. If the cell is empty, the critter goes to that cell. If the cell contains a plant, the critter moves to the cell and eats the plant in the process. If the cell contains a rock or another critter, the critter "bumps" into the object and stays where it is.
Each critter starts with an initial strength of 3000. When the critter takes an action, it receives an reinforcement, which is added to its current strength (except that the strength can never exceed 3000). There are four possible reinforcements that are built into the world in the learning version of the program; you can change any of these by selecting "Change params" in the Control window.
You can also change the two parameters that control Q learning: the discount rate (γ in the Q learning rule) and the learning rate (η in the neural network version of the Q learning rule above). And you can change the parameter that controls how the rate of exploitation changes with critter age (E in the exploitation-exploration equation above).
Each critter has its own neural network, in which it learns the weights that implement Q values based on its experiences. Each neural network learns independently of all of the others. You can see a visual representation of a critter's neural network by clicking on the critter. The input to the network is displayed in the column on the left side of the window (you will need to scroll down to see all of it); each square represents a single neural network unit with the size denoting the activation. There is a unit for each state feature, that is, for each of the four possible textures in the position of each of the critter's six touch sensors. The row at the top of the window represents the target for the current input. For the unit representing the action taken, this is what the Q learning rule would predict for the Q value for that action in the current state; the size of the square denotes the magnitude of the value, and the color denotes its sign (green for positive, red for negative). For the other units, no value is shown. Below this row is a row of squares showing the current activations of the output layer of the neural network. In the rest of the window are the weights associating input and output units.
You can watch learning take place in a single critter by opening its neural network window and then clicking on the Step or Run buttons in the Control window.