Jan 27, 2000

For a good introduction to basic acoustics and hearing, see the McGill Univ audition site. In particular, read their page Basic Acoustics and Psychoacoustics, which is similar in content to the page below.

1. WAVE MOTION: vibration (oscillation) of particles in a medium

A. the acoustic medium must contain particles that are elastic, that is, sloshy or springlike.

B. The motion of each particle sets adjacent particles in motion. Energy is transferred over great distances by small local motions of particles.

C. Types of waves: Differences in motion of particles with respect to motion of the wave front. All exhibit the same abstract properties.

1. Transverse. Particles move perpendicular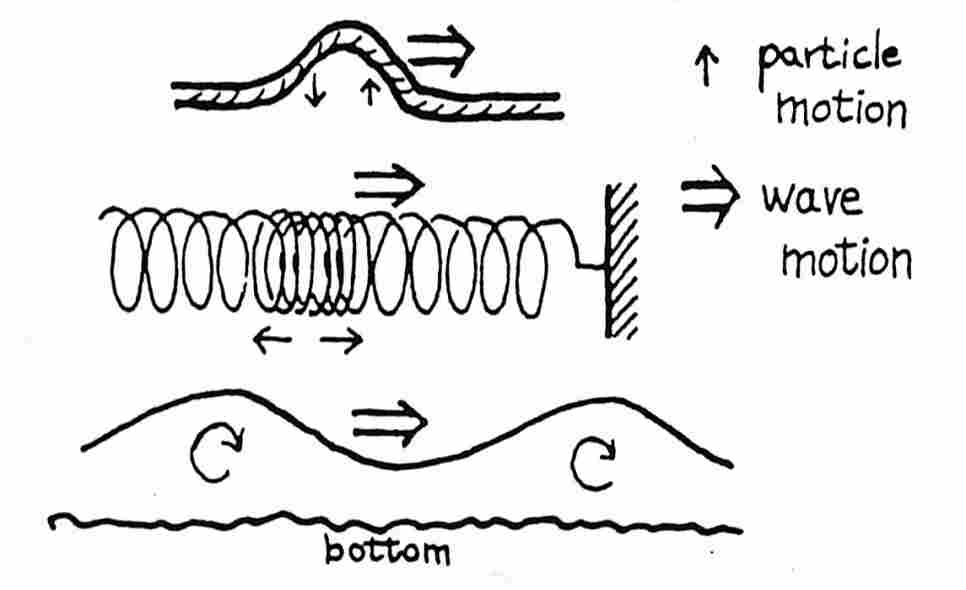
to wave front. Like a wave in a rope or slinky.
2. Longitudinal. Particles move forward/backward re wave front. Like sound (or slinky).
3. Combination waves. Both horizontal and perpendicular motion. Like familiar surface waves on water.
4. Varying number of dimensions for the medium:
1D (on a line, like rope or wire), 2D (on a surface, like ripples on pond), 3D (in a volume, like sound in air, earthquakes in the planet). The behavior of the waves is fundamentally the same for all of these, despite the differences.

2. WAVE CYCLE AND GRAPH

When air (for example) is still, it has some pressure that is measurable with a barometer but not detectible by human sensory systems. For the study of sound, this pressure is considered to be zero. If something disturbs the air, it typically results in the cyclic changes in the pressure around this zero which our ears are sensitive to.

A. Period (T) of a wave is duration between any point 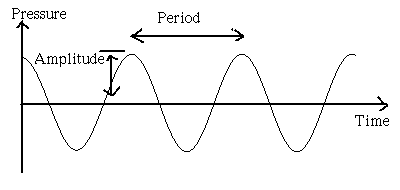on a wave and the same point on the next cycle. Measured in milliseconds for audible sounds. T = 1/f. Notice there is as much negative portion as positive portion of a wave (so that the mean is the pressure of still air (or whatever).

B. Frequency (f) is the number of cycles per second. f = 1/T. Often it is measured in thousands of Hz = kHz (at least in the auditory range).

C. Amplitude (A) of a wave, the instantaneous pressure or displacement of particles in the medium. The amplitude has no relation to wave speed or its frequency. A given sound with greater amplitude sounds louder than the same sound with smaller amplitude.

D. Velocity of wave front motion (s) depends solely on the medium. Thus it is independent of A, T or f. Waves of any frequency move at the same very low velocity in a slinky but faster in air and faster still in water and steel.

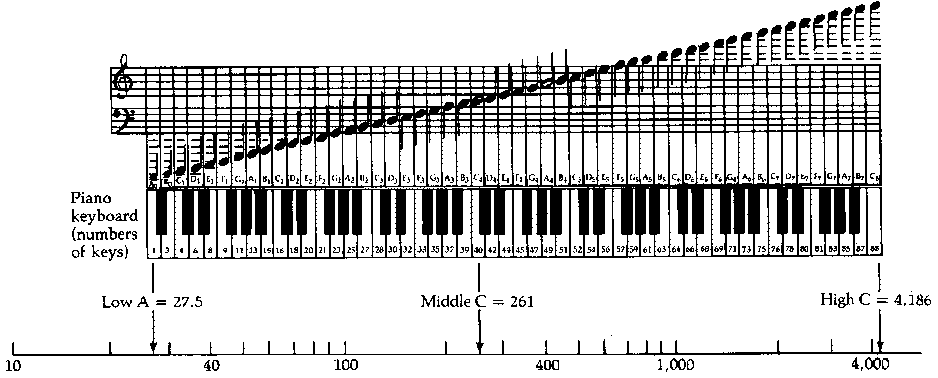
3. Sound is wave motion, typically of air, in the (humanly audible) frequency range of 20 Hz--20 kHz. The figure below of a piano keyboard and the musical gamut shows at least the range of musical sounds. You can see that the musical scale is logarithmic and that the highest note on a piano is about 4kHz (still over 2 octaves below the highest frequency we can hear). The lowest note (at 27.5 Hz) comes close the lower limit of hearing. The fundamental frequencies of adult human speech normally lie between about 75 Hz and 400-500 Hz.

4. WAVEFRONT MOTION

A. Propagation. Waves keep on going once initiated. However, in 2D or 3D media, their amplitudes get smaller as they spread since the energy gets distributed over greater and greater distances.

B. Diffraction. Waves bend around corners. But low frequencies bend better than high frequencies. Thus in the middle panel below, only low frequencies will spread like those shown. As frequencies get higher, the tend to beam straight ahead and not spread to the right and left.

C. Reflection. Waves reflect partially when resistance of medium increases.

D. Additivity (or superposition). When several waves are in the same place at the same time, they just add to each other at each moment in time. Since (+4) plus a (-4) = 0, it is possible for two sounds to add up to no sound at all - as long as they always have the opposite amplitudes at some single location.

5. SOME WAVE TYPES

A. Pure tone or `simple sound.' The wave looks like a `sinusoid' curve. (See the second figure above.) It is the simplest possible wave shape - mathematically, the projection of fixed-rate circular motion onto a perpendicular plane.

B. Complex waves: the sum of two or more sinusoids, usually harmonically related (that is, integer multiples of a `fundamental frequency', the f0).
1. harmonic sounds: They sound like a hum or buzz, they have a clear pitch.
2. nonperiodic sounds: eg, nonharmonic tones (eg, bell which seems to have several different pitches) and noise (hiss or whoosh)
3. fundamental frequency - the lowest frequency component of a complex wave. It has this name both because this frequency `generates' all the others and because typically this is the auditorily heard pitch of a complex tone.

C. Fourier's Theorem: "Any wave that is periodic can be represented as the sum of sinusoidal components whose frequencies are integer multiples of the fundamental period with appropriately chosen amplitudes. "

D. Spectrum Display: a graph showing the sinusoidal components that are summed to equal some sound wave.

6. SOUND SPECTRA and ANALYSIS FILTERS

A. Filters. Since sound is always a sum of independent frequency components, specific frequencies can be added to OR subtracted from any sound. Various mechanical and electronic devices, called acoustic filters, can strengthen or weaken selected frequencies relative to other frequencies. Many things can be acoustic filters, for example, a physical tube, a room, a loudspeaker, a microphone, etc.

B. A Sound Spectrogram is a graphic display of the sinusoidal components of a sound. These displays are very useful for understanding speech sounds.

For more on speech spectra, check Port's speech acoustics page and the speech web references on the syllabus page.